Hello! Welcome back to the Smartick blog. In this post, we will look at how to get the sums of fractions. You will see how easy it is for you.
To get the sums of fractions, it is necessary that each fraction has the same denominator.
Sums of fractions with the same denominator:
In this case, the sum is very simple, because we just have to add the numerators leaving the denominator that they have in common.
For example:
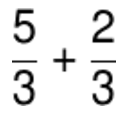As the two fractions have the same denominator, we just have to add the numerators, keeping the same denominator.
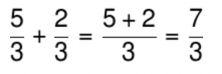Isn’t that easy?
Sums of fractions with different denominators:
In this case, we need the two fractions to have the same denominator. How do we do it? We must find the least common multiple (LCM) between the 2 denominators. After changing the denominators, what do we do with the numerators? We rewrite the result as a fraction equivalent to the first fraction.
Once we have the two fractions written with the common denominator, we can now add them, as we did in the previous section.
For example:
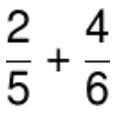To perform this problem, you must calculate the LCM between 5 and 6 first.
LCM (5, 6) = 30
Therefore, the new denominator of the fractions is 30.
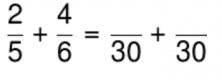
Now we must find equivalent fractions: multiply the numerator by the same number as the denominator:
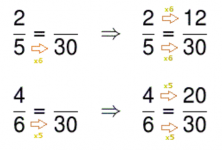Now we can figure out the sum of the fractions.
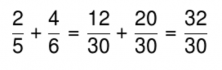Finally we simplify the fraction by dividing the numerator and denominator by 2:
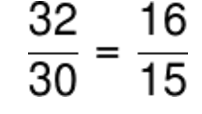Did you like this post? Well, feel free to share with your colleagues and friends so they can also learn to solve for the sums of fractions!
To keep practicing getting the sums of fractions and all elementary math topics, sign up for Smartick free trial.
Learn More:
- Two Ways of Dividing Fractions and Some Examples
- How to Find a Sum of Fractions
- Learn and Practice How to Subtract or Add Fractions
- Learning How to Subtract Fractions
- Learn and Practice How to Multiply Fractions
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.
- Mathematical Formulas: What Are They, How Are They Made and Types of Formulas? - 11/29/2024
- The Language of Functions and Graphs - 07/01/2024
- Educational Technology: The Christodoulou Test - 05/06/2024