In today’s blog post, we are going to look at scales and their importance in mathematical logic. We will also check out some exercises involving scales that appear in Smartick sessions. Finally, we will examine the usefulness of scales in understanding the equal sign as equivalence in algebraic equations.
Index
What Is a Scale?
A scale is a tool that helps us compare and measure the weight of different objects. Teaching concepts such as balance, weight measurement and equivalences using scales plays a crucial role in the development of mathematical logic. In addition, when we use this tool, it provides a visual representation of equality. Thereby, allowing for a concrete understanding of how two sides are equal when balanced, which is essential for grasping mathematical equations.
On another note, working with scales fosters problem-solving skills when confronted with how to balance the scale. This hands-on approach also facilitates the application of mathematical operations, such as addition and subtraction, by demonstrating how adding or removing weight affects balance.
The primary function of a scale, however, is weight comparison. By placing objects on both sides of the scale, you can determine which is heavier, lighter, or if both have the same weight. This facilitates the relative comparison of different materials. Now, imagine two plates, one at each end of a horizontal bar. You can place one object on one plate and another object on the other plate. If one side is lower than the other, it means that, that object is heavier. If both sides are at the same level, the two objects have the same weight!
When both sides of the scale are at the same level, it indicates that the weights are equal. This concept of scale is fundamental and has practical applications in solving weight problems and comparing quantities.
Scales in Smartick Exercises
Now, let’s look at two balance exercises that appear in Smartick sessions.
Example 1
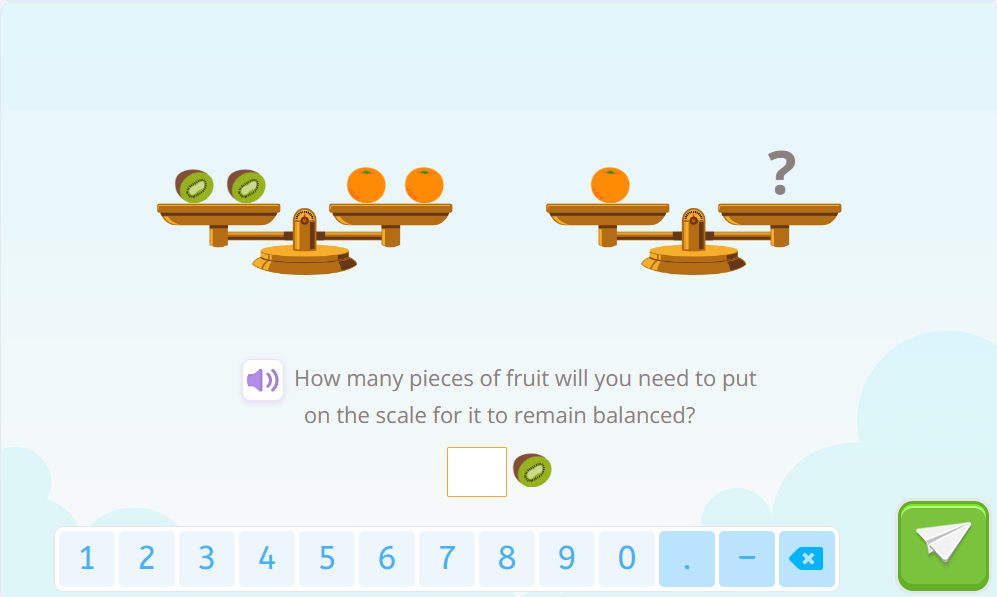
We have to look at the plates of the first balance of the exercise and find the relationship between the weight of the objects on one plate and the weight of the objects on the other plate. The first scale is in balance when we have two kiwis on the left plate and two oranges on the right. This would therefore mean that one kiwi weighs the same as one orange.
Now, to balance the second scale, let’s examine the fruits on the left plate. There’s only one orange, and we know the weight of one orange equals that of one kiwi. Hence, to balance the second scale, you only need to place one kiwi.
Example 2
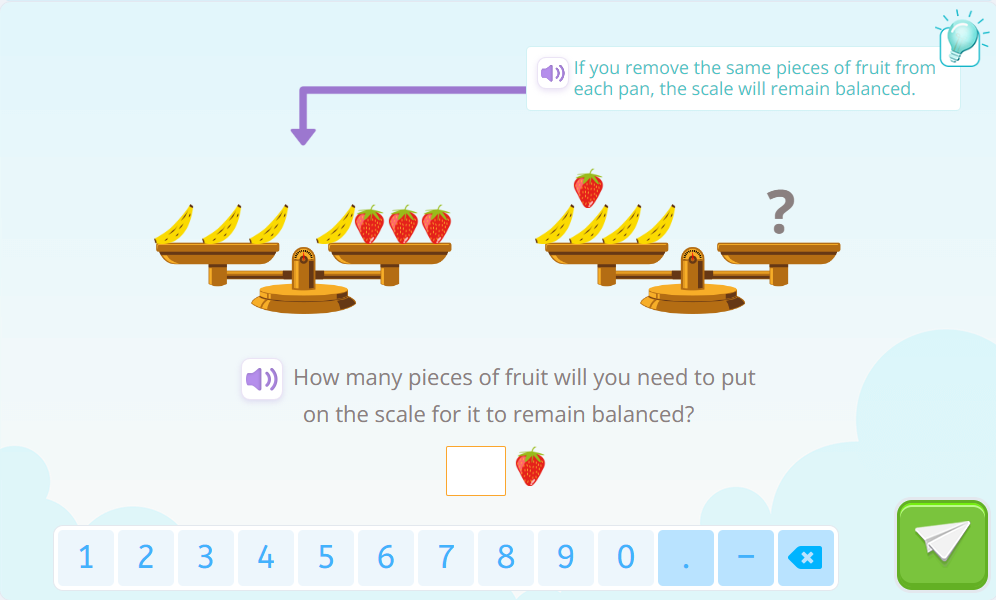
Again, let’s look at the plates of the first exercise’s scale and find the relationship between the weight of objects on one plate and those on the other. Look! There’s a clue in this exercise: “If we remove the same pieces of fruit from each plate, the scale remains balanced.” In this case, removing a banana from both the left and right plates. By eliminating the common pieces from both plates, we see that the weight of two bananas is equal to the weight of three strawberries.
So, if we want to balance the second scale, let’s focus on the fruits on the left plate. There are four bananas and one strawberry. Since two bananas equal three strawberries, we replace the four bananas with six strawberries, and to balance the scale, we need to add one more strawberry. In total, 7 strawberries are needed.
Now that you have seen two examples, dare to tackle the following proposed exercise?
Proposed Exercise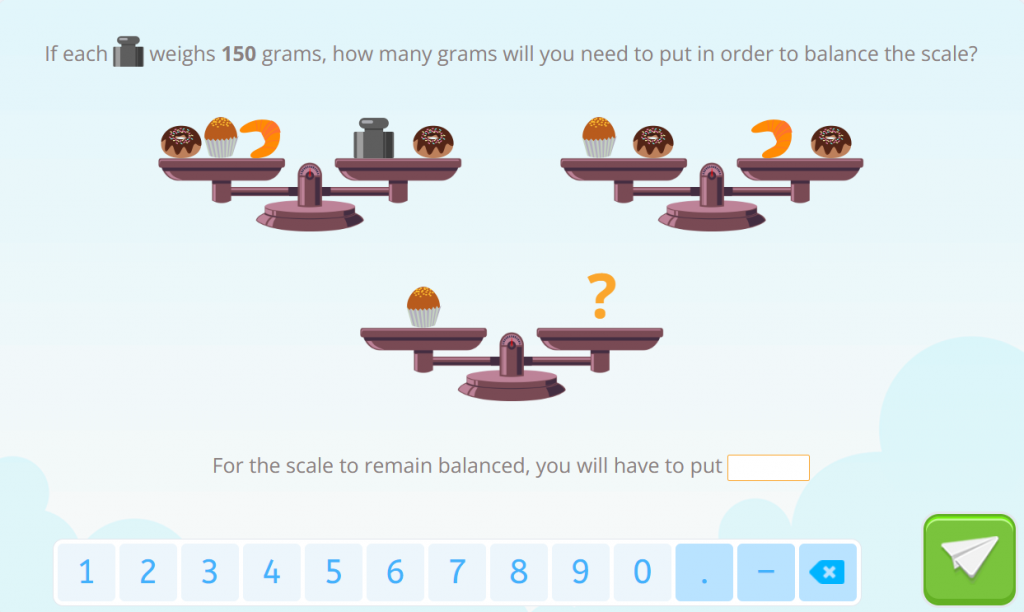
Solution to the proposed exercise: 75 grams.
Scales and Algebraic Equations:
As we have said before, balances allow the visualization of algebraic equations through the analogy of being in balance using a scale.
Until we come into contact with algebra, we often perceive the equal sign as instruction for an operation to we perform. However, when we are confronted with an equation and see two sides that are not directly related by an arithmetic operation, understanding the new meaning of equality as a balance for a specific value can be tricky. Now, the equal sign is not an instruction, but rather a concept of balance that only holds true for a particular value of a variable.
That’s where the scales come into play. They help us understand this new meaning of the equal sign. We need to view equal signs as scale, and scales become an incredible tool to understand this new sense of balance. So who would have thought that scales could be key to understanding algebra and the intriguing world of equations?
Let’s take a look at an example of how we can represent a simple first degree equation with a scale. For this, we will use the free tool “balance” from Mathigon, found in the Algebra section. Look at the image below; it is an analogy of the equation 2x+2=8 using a scale:
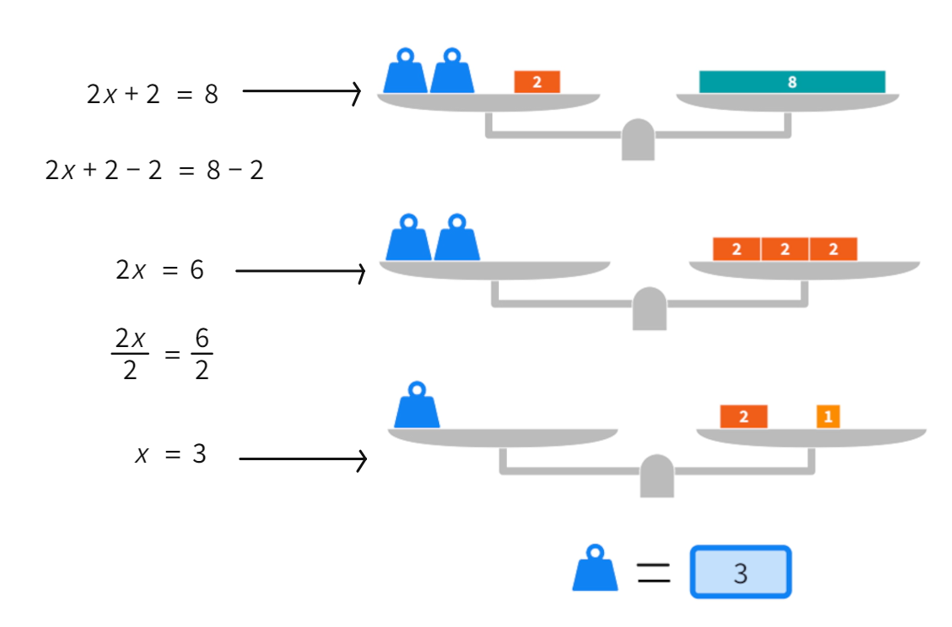
In the following video, you can check out how to solve the equation step by step using a scale:
You can try to use scales to solve the equations that they have as examples on Mathigon.
If you found this post interesting, feel free to share it or drop your questions, concerns, or topics you’d like to know more about in the comments. To learn more, register in Smartick, the online method for learning math and reading comprehension for children from 4 to 14 years old.
Learn More:
- Why Are Examples Important When Teaching Mathematics?
- Introduction to Equations with an Example
- Logic Exercises at Smartick and a Math Riddle
- Reducible Equations: What Are They? How Do We Solve Them?
- Learning the Temperature Scales: Degrees Celsius or Fahrenheit?
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.