We will continue reflecting on Craig Barton’s book How I Wish I’d Taught Maths on the Smartick blog. Today, we will address the topic of diagnostic questions in mathematics education.
Diagnostic Teaching
Diagnostic teaching has a long tradition in mathematics education. This approach to teaching mathematics was initially developed in the 1980s, at the University of Nottingham’s Shell Centre by researchers such as Hugh Burkhardt and Malcolm Swan. The International Commission on Mathematical Instruction (ICMI) recognized this work in 2016, and awarded both researchers the first Emma Castelnuovo Award for Excellence in the Practice of Mathematics Education.
Diagnostic teaching is a method of formative assessment for learning that combines research with curriculum development in mathematics. Diagnostic questions play quite a crucial role in diagnostic teaching.
Diagnostic Questions
Diagnostic questions are closed, multiple-choice questions. Which allow students to precisely identify and understand their errors and misconceptions when learning math. These questions help teachers quickly detect their class’s overall level, and which aspects of a topic are crucial to focus on. The questions form the initial diagnostic method and are designed based on results from research on student learning difficulties in math.
Errors in Mathematics
One of the goals of using diagnostic questions is to differentiate between when a student simply makes a mistake, and when they make a mistake due to misunderstanding. Math errors aren’t really errors. They are usually due to a lack of attention, but they are not systematic. A student can get confused and say that 7 plus 6 is 12, after counting on their fingers from 7. Surely, the next time they calculate the same sum they will do it correctly, and not require assistance to correct this “mistake.” However, errors reflect a pattern, as they are the result of poor or incomplete knowledge. Errors are usually persistent and reappear even after explicitly attempting to correct them.
Errors When Using the Equal Sign
We know that using the equal sign leads to persistent difficulties and mistakes. One of them occurs when we link two arithmetic operations together. By asking students to mentally calculate 8 + 5, many may respond, “Eight plus two is ten, plus three, is thirteen.” If we then request that they write this calculation down in their notebooks, many may write 8 + 2 = 10 + 3 = 13. The right thing to do, in this case, would be to separate the two equations like this: 8 + 2 = 10; 10 + 3 = 13. This type of mistake is very common – first in elementary school arithmetic, and then again in high school algebra. The equation, 8 + 2 = 10 + 3, is not correct because the left side equals 10 and the right equals 13, meaning both expressions cannot be linked with an equal sign.
Examples of Diagnostic Questions on Smartick
Smartick presents exercises to students, at the beginning of their algebra sessions, which follow the approach of diagnostic questions. The following exercise tries to assess if two products, with two nonzero factors, are understood to match one of the factors in both products. They can only be the same if the other factor matches. However, in this case, we are dealing with an example of the commutative property of the product. Therefore, only the first option among the following correctly represents the equation. The same would happen with the addition a + b = c + b. The equation can only be correct if a = c.
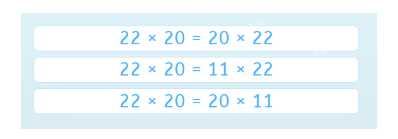
Here’s another example of a diagnostic question that requires selecting the correct options. With questions like this, we can quickly assess if students know the commutative property of addition (Option B). But keep in mind that this property does not apply to subtraction (Option C).
How Diagnostic Questions Help When Planning New Topics
In what situation will these types of exercises become diagnostic questions? When we’re going to start solving first-degree equations, and there is interest in differentiating cases in which equations have one solution, infinite solutions, or none. The knowledge of the equal sign that we evaluate, in diagnostic questions like those previously, is what allows us to distinguish between these cases without performing operations. Thus, in case (1), the equation does not have a solution, since 3 is not equal to 2. In equation (2) we have a single solution (x=0), and equation (3) has infinite solutions, as it is correct for any value of x. This little assessment allows teachers to determine if students have the prior knowledge necessary for understanding the equal sign. Otherwise, teachers may want to review it, so that they can address the introduction to equations with a higher guarantee of success.
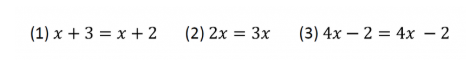
During Smartick’s daily sessions, there are several diagnostic questions presented to assess each student’s level of mathematical competence. This allows us to offer our students the best, personalized route for learning mathematics. One which takes into account the possible strengths and weaknesses of their mathematical thinking.
Learn More:
- Introduction to Equations with an Example
- The Associative Property and Mental Math
- Scales in Mathematics: What Are They and What Are They Used For?
- Reducible Equations: What Are They? How Do We Solve Them?
- Why Are Examples Important When Teaching Mathematics?
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.