In order to subtract or add fractions, we must have the same denominator.
We can see this in different cases:
- Subtract or add fractions with the same denominator: If both fractions to be added or subtracted have the same denominator, we leave the same denominator and add or subtract the numerator.
We are going to look at an example. If we add 7/10 and 10/10, we leave 10 as the denominator of the resulting fraction and we add the numerators, 7 + 10 = 17. The result of the fraction would be 17/10.
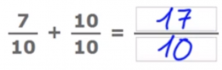
- Subtract or add fractions with coprime denominators (that do not have common factors): In order to calculate the sum or difference of this type of fractions, we will have to multiply the denominators in order to find the denominator of the resulting fraction. To get the numerator, we would have to multiply the numerator of one of the fractions by the denominator of the other and vice versa, and afterwards, add or subtract the result, depending on the type of operation that we have to carry out.
Here is an example: We add 11/10 + 2/3.
The denominators are 10 and 3, which are different and do not have common factors, so we will have to multiply them. 10 x 3 = 30, therefore 30 will be the denominator of the resulting fraction.
In order to calculate the numerator, we will have to multiply 11 x 3 = 33 and 10 x 2 = 20, and add the results, 33 + 20 = 53, which would be the numerator of the answer.
The final answer to the addition would be: 53/30.
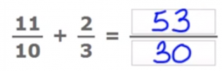
- Subtract or add fractions with a denominator which is the divisor of the other:
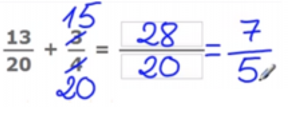
We are going to see an example in order to clarify. We are going to add 13/20 + 3/4.
The denominators of these fractions are different, but since 4 is a factor of 20, we can multiply the 4 by a number that gives us 20, which is 5. We multiply both the numerator and the denominator of 3/4 by 5 and we are left with 15/20 and we find the sum of both fractions, which gives us the answer 28/20. But 28/20 can simplify, as 28 and 20 are multiples of 4, so we divide the numerator and denominator by 4, giving us 7/5 as a final answer.
- Subtract or add fractions with the least common multiple:
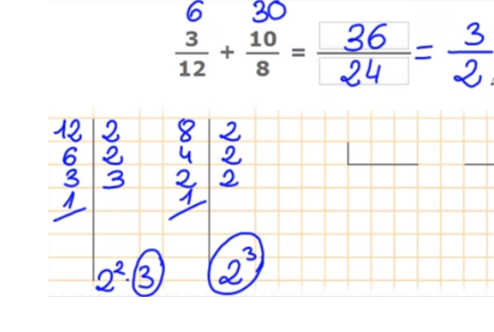
We are going to continue with an example. We are going to add 3/12 + 10/8.
12 and 8 are the denominators of the added fractions, which are different but have common factors. Therefore we are going to factor the numbers in order to determine the least common multiple, as shown in the image.
In order to calculate the least common multiple, we multiply the factors, using the highest power of any common factors.
Therefore, the common denominator is 24.
Now, in order to calculate the numerator of each of the fractions that we are going to add, we divide the calculated least common multiple into the denominator, and we multiply the answer by the numerator.
24/12 = 2 3 x 2 = 6 Resulting fraction: 6/24
24/8 = 3 10 x 3 = 30 Resulting fraction: 30/24
And we add the numerators of both fractions, so the sum of the two fractions is 36/24.
But this fraction can be simplified if we divide the numerator and denominator by 12. The irreducible fraction would be 3/2.
After adding or subtracting the fractions, learn how to simplify the fractions by the lowest terms!
You can also practice word problems with fractions.
To keep learning, try Smartick free trial!
Learn More:
- Two Ways of Dividing Fractions and Some Examples
- Learn How to Subtract Fractions
- Learning How to Subtract Fractions
- Learn and Practice How to Multiply Fractions
- Learn How to Divide Fractions with Two Different Methods
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.