In this post, we are going to explore the Pythagorean theorem and some of the proofs. Finally, we will look at how to solve a problem by applying this theorem.
What is the Pythagorean Theorem?
A theorem in mathematics is a proposition or statement that can be proved logically and rigorously, using mathematical rules and principles. A theorem is always valid and is used to establish fundamental truths in mathematics.
The Pythagorean theorem has this name because the evidence, above all, is an effort of the Pythagorean school. Pythagoreanism was a philosophical and mathematical trend associated with the Greek thinker Pythagoras, who lived in the 6th century BC. Although it is difficult to separate the real historical aspects from the tales surrounding Pythagoras, he is credited with founding the Pythagorean school where, despite the period, both men and women could study. They studied mathematics for the satisfaction of contemplating and solving mathematical problems at a time when only architects and engineers were obliged to study it.
The Pythagorean theorem states that, in a right triangle, the area of the square whose side is the hypotenuse is equal to the sum of the areas of the squares on the other two sides.
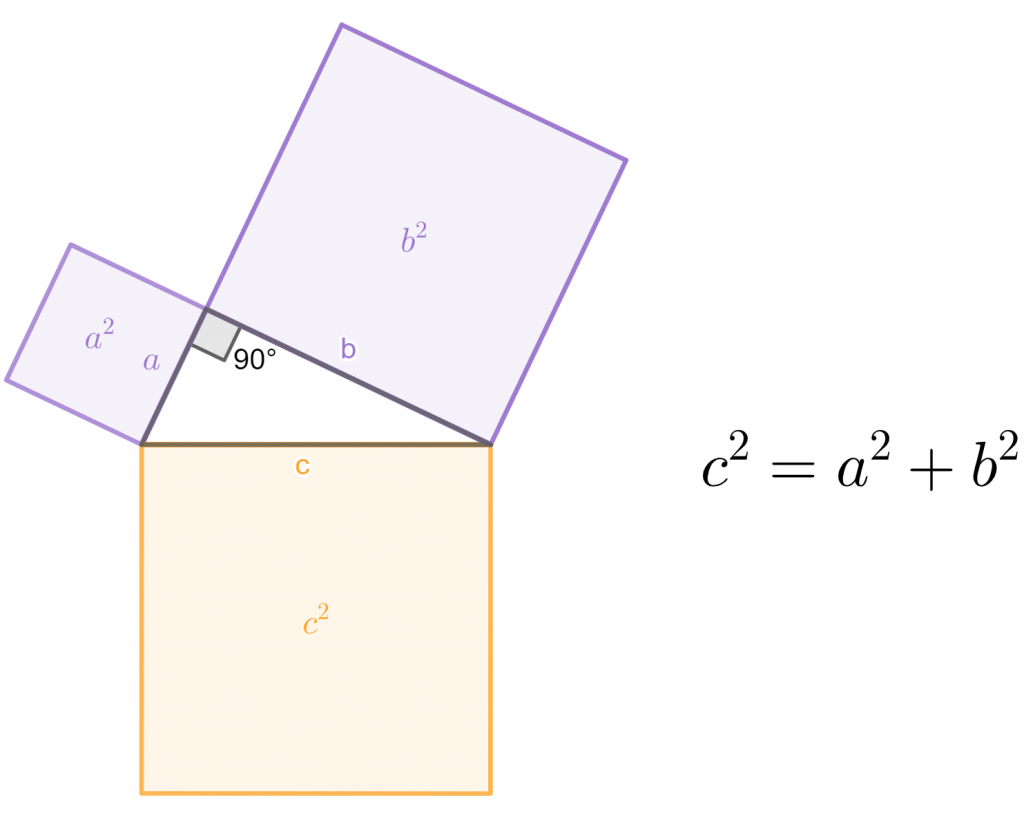
In a right triangle, the minor sides are those that form the right angle and are called legs and the major side is called hypotenuse. In the right triangle in the image:
- a and b are the legs
- c is the hypotenuse
Proofs of the Pythagorean Theorem
The Pythagorean theorem has been proved in various ways throughout history, and there are numerous proofs. Each proof presents different mathematical approaches and concepts, and we will now look at three of them:
- Proof of the Pythagorean theorem using Montessori strips.
52=32+42
25=9+16
25=25
- Proof of the Pythagorean theorem using Tangram pieces.
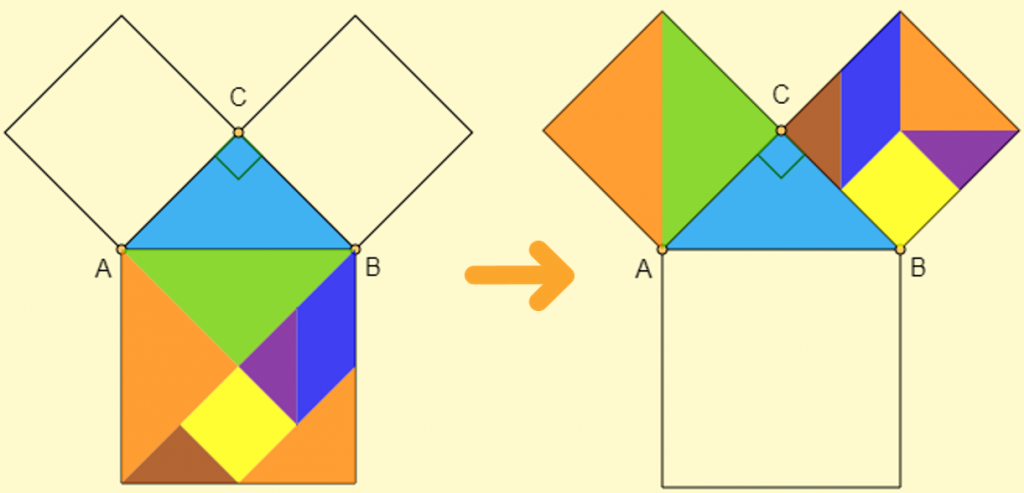
In the following video you can see the interactive demonstration:
- Perigal’s proof of the Pythagorean theorem. The English mathematician Henry Perigal (1801/1898), is credited with an ingenious proof of the Pythagorean theorem. “On the largest of the squares built on the legs, the center is determined and two straight lines are drawn parallel and perpendicular to the hypotenuse of the triangle. With the four pieces obtained plus the square built on the other leg we can cover the square built on the hypotenuse.”
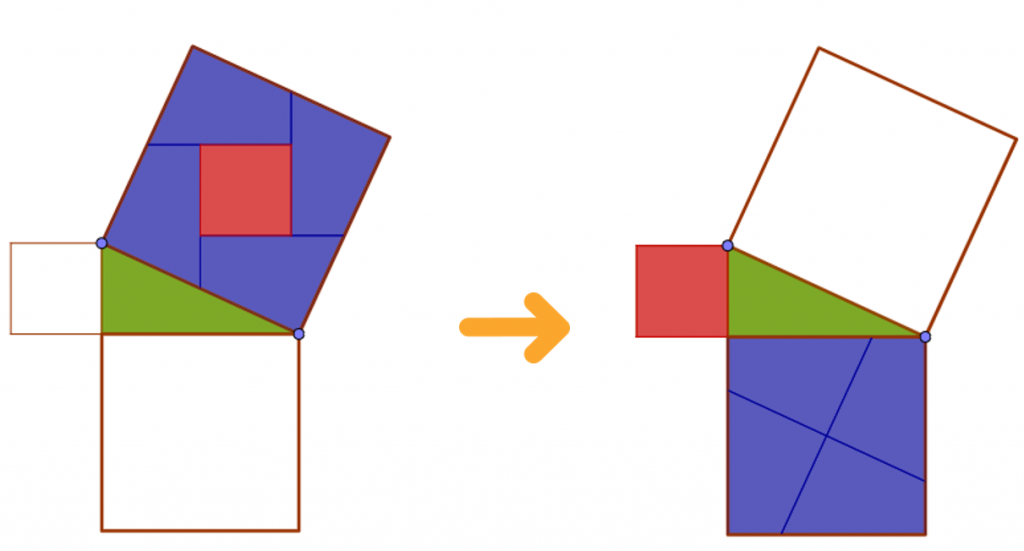
In the following video you can see the interactive demonstration:
Solving Problems Using the Pythagorean Theorem
Having seen what the Pythagorean theorem is and some of its proofs, let’s look at an example of a problem that is solved using the Pythagorean theorem.
Problem statement:
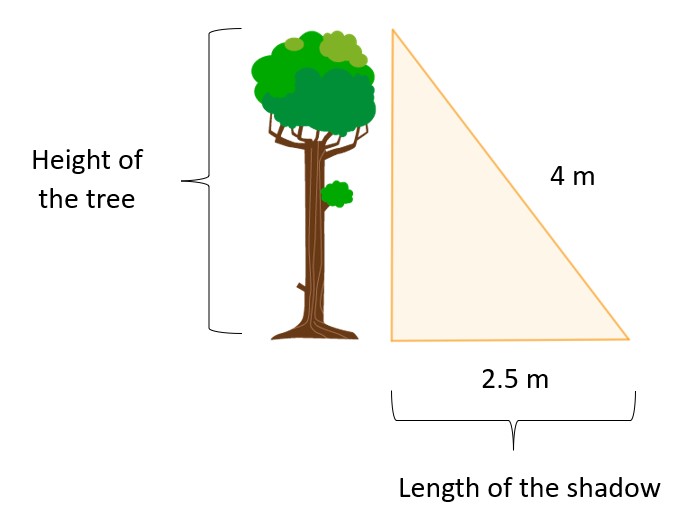
We want to measure the height of a tree. At a certain time of the day, we notice that the shadow of the tree on the ground measures 2.5 meters. In addition, we measure the distance from the top of the tree to the end of the shadow on the ground, and that distance is 4 meters. What is the approximate height of the tree?
Solving the problem by applying the Pythagorean theorem:
To calculate the height of the tree, we can use the Pythagorean theorem. In this case, we must identify which sides of the right triangle formed by the shadow, the tree and the distance joining their points. From here, we can assume that the tree is perfectly straight, otherwise the triangle would no longer be a right triangle and we could not use the Pythagorean theorem.
The height of the tree and the length of the shadow are the legs of the right triangle and the distance between the highest point of the tree and the shadow would be the hypotenuse.
- a is the height of the tree
- b is the length of the shadow
- c is the distance from the tip of the tree to the end of the shadow
c2=a2+b2
42=a2+(2,5)2
a2=42-(2,5)2
a=3,12
So, the approximate height of the tree is 3.12 meters. To attempt this kind of problems it is necessary to know how to solve quadratic equations and to remember how to round decimal numbers.
I hope you have found this post to be interesting. Feel free to share or leave your comments, questions, concerns or the topics you would like to learn more about in the comments below. To continue learning, register in Smartick, the online method for learning math for children from 4 to 14 years old.
Learn More:
- Curiosities of Some Geometric Figures
- Geometric Plane Shapes: Circles, Triangles, Rectangles, Squares, and Trapezoids
- Learn the Properties of Geometrical Prisms
- How to Calculate Perimeters: Part 1
- Perimeter: What Is It and How to Find It for Any Polygon
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.
- The Language of Functions and Graphs - 07/01/2024
- Educational Technology: The Christodoulou Test - 05/06/2024
- Multiplication Activities in Smartick - 04/09/2024