Today we are going to learn to calculate perimeters of geometric figures. But first, let’s start with the definition of a perimeter. When we say perimeter we are referring to the length of the polygon’s outline.
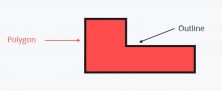
Here you can review the most common types of polygons.
The length of a polygon’s outline can be calculated by adding together all of the segments that form its sides.
Calculate the perimeter of any polygon
I am going to show you the first strategy for calculating perimeters where the number of sides a polygon has is not important.
The perimeter of a geometric figure can always be calculated by adding together the length of each side.
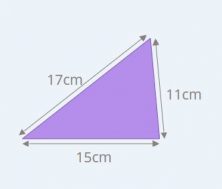
For example, you can calculate the perimeter of this triangle in the following way.
Perimeter = 17cm + 15cm + 11cm = 43cm
You can use this strategy to calculate the perimeter of any polygon.
Calculate the perimeter of squares
The special characteristic of a square is that it has four equal sides. We can take advantage of this by simplifying our calculations.
You can calculate the perimeter of this square by adding together the lengths of the four sides.
Perimeter = 6cm + 6cm + 6cm + 6cm = 24cm
Since the four sides are equal, multiplying the length of one side by four will give you the same result.
Perimeter = 4 x 6cm = 24cm
So, you’ve discovered a rule to help you with any square.
Perimeter of a square = 4 x side length
Calculate the perimeter of rectangles
In every rectangle, the opposite sides are equal to one another. It has sides that are equal, two by two.
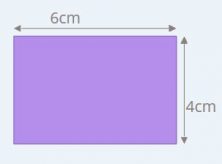
In order to calculate the perimeter of the rectangle in the example, you can add the length of its sides, two 6cm sides, and two 4 cm sides.
Perimeter = 6cm + 4cm + 6cm + 4cm = 20cm
You can multiply the sum of the base and height by two and obtain the same result because all rectangles repeat the length of their sides two times.
Perimeter = 2x (6cm + 4cm) = 20cm
So, you have an approach for any rectangle.
Perimeter of a rectangle = 2 x (base + height)
Calculate perimeters of equilateral triangles
The same as with squares, the sides of an equilateral triangle are equal. They all measure the same length.
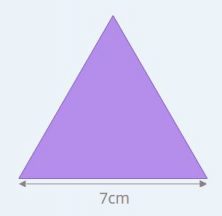
Each side measures 7cm and you can calculate the length of its outline in the following way.
Perimeter = 7cm + 7cm + 7cm = 21cm
Or, there is an easier way. Since the three sides are the same, you can multiply one side by 3 and the result does not change.
Perimeter = 3 x 7cm = 21cm
And this helps you with an equilateral triangle.
Perimeter of an equilateral triangle = 3 x length of one side
Calculate perimeters of any regular polygon
The defining feature of regular polygons is that all of their sides are the same length.
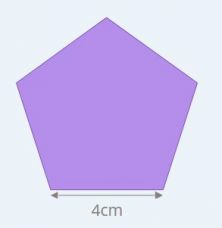
Since a pentagon has five equal sides, to find its perimeter you multiply the length of one side by five.
Perimeter of a pentagon = 5 x length of one side
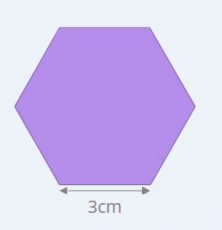
And with a hexagon, which has six equal sides, you can multiply one side by six.
Perimeter of a hexagon = 6 x length of one side
From these rules, we are able to extract a rule to calculate the perimeter of any regular polygon in a simple way.
Multiply the number of the sides of the polygon by the length of one of the sides.
Perimeter of a regular polygon = nº of sides x length of one side
If you would like to learn more about perimeters, geometry, and other topics like finding least common multiple in primary mathematics, log on to Smartick and try it for free.
Learn More:
- Perimeter: What Is It and How to Find It for Any Polygon
- How to Calculate a Perimeter: Part 2
- How to Calculate the Area?
- Calculating the Area of Polygons
- Geometric Plane Shapes: Circles, Triangles, Rectangles, Squares, and Trapezoids
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.
- The Language of Functions and Graphs - 07/01/2024
- Educational Technology: The Christodoulou Test - 05/06/2024
- Multiplication Activities in Smartick - 04/09/2024
Great work, well done
Thanks 🙂
Interesting and ready to learn
This is very educative, thanks
Bravo Glad I found this
very helpful and easy to access thank you