Geometry is seen in school as a collection of formulas that answer the question, how to calculate the area? Geometry is much more than that: it comprises the whole part of mathematics that solves problems of space, answers questions about the shape of plane and three-dimensional figures and, it goes much further, trying to answer the shape of our universe… But let’s not go that far, before answering this question, it is important that we know about what we mean when we ask ourselves about the area of a polygon.
Index
Confusion between Area and Perimeter
When we are asked about an area we are being asked about the surface, not about what surrounds it. A very typical confusion is, instead of measuring or calculating the surface, we measure “what surrounds it”, the perimeter.
In a rectangular painting with a thin metal or wooden frame, the area would be the painted part, the canvas or paper, while the perimeter would be the length of the frame.
In the video below, another example is used, a vegetable garden made with several surfaces in which different crops are going to be planted. Stakes are placed in their vertices and ropes delimit them. In this scenario, the length of these ropes would be the perimeter.
The perimeter is always a measure of length.
Videotutorial on How to Calculate the Perimeter of Any Figure
In this Smartick videotutorial you can learn in a simple way how to calculate the perimeter of any figure.
Having cleared up, I hope, the possible confusion, I recommend that you read: How to calculate the perimeter? If that is what you are interested in.
How to Calculate the Area of a Polygon on a Grid?
If the polygon you want to know the area of is in a grid, there is a very simple way to calculate its area: count the squares it covers. But be careful, the areas are surface measures, and therefore, you must also indicate the units. They can be square meters, square centimetres… they will always be square units, because they come out of the square count we were writing about.
Now, look at the following example, because there is a detail that you cannot overlook:
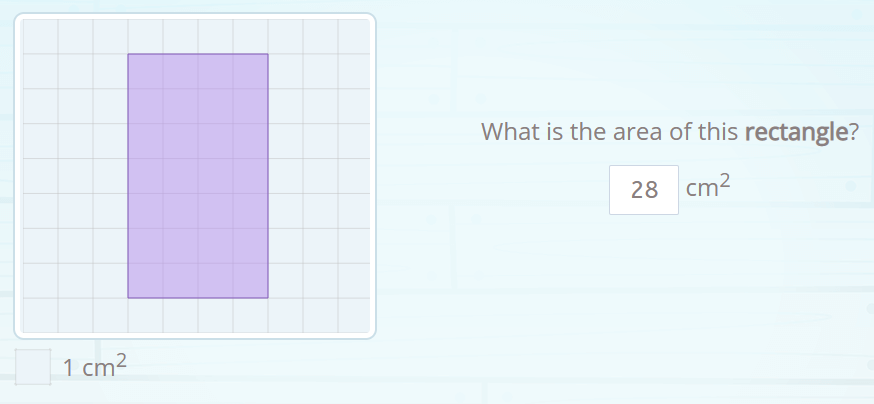
Below the grid, there is a little square that tells us how much each square measures, it is the legend of this figure, and tells us that each square is equal to one square centimetre. But it could be different and it could be equal to a square meter (if it were the plan of a room) or a square kilometre (if it were the map of a region) or it could be that each square was 2 cm² and then the area of the rectangle would be 28 by 2, 56 cm².
This simple way to answer how to calculate an area can be applied when the figure is composed of several polygons, which is called a compound polygon. As in the example below:
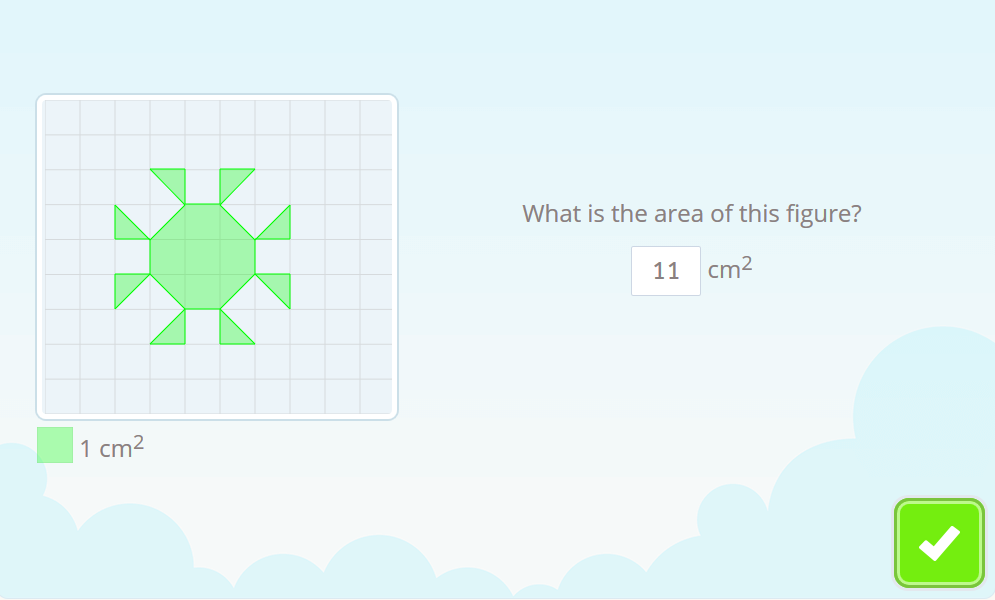
In this case we will have to count squares and half squares.
How to Calculate the Area of a Rectangle?
Counting squares is fine, but if there are a lot of squares you may skip some or count them twice. If the figure you want to know the area of is a rectangle there is a faster way. Think about it, in rectangles, the squares are organized in rows and columns. So, if you want to know how many squares are there, you just have to… multiply the number of rows by the number of columns!
What if there is no grid underneath but you know the width and height of the rectangle? Well, since it was to see how many unit squares were in the rectangle, there will be as many as the product of the width times the height, the famous base times height.
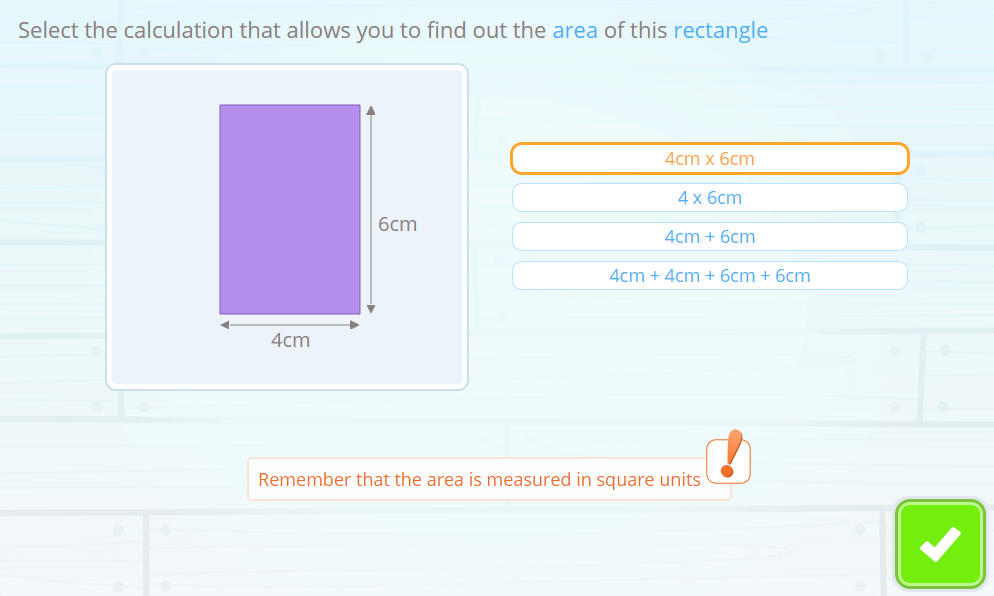
You will have to make sure that the two measurements are in the same unit, that is, both in centimetres, in decimetres, in meters… This way you will be able to know the area units as well: square centimetres, square decimetres or whatever, but square.
Area of a rectangle= base × height
How to Calculate the Area of a Right Triangle?
The simplest case is that of the right triangle. Think about it, a right triangle is half a rectangle, the one that is divided by its diagonal.
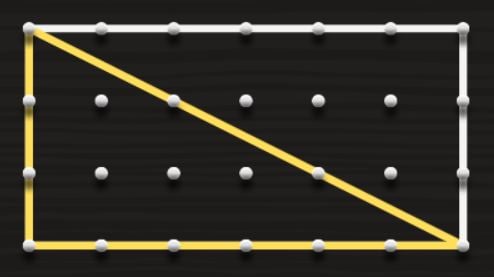
As we already know from the previous section, the area of the rectangle is calculated by multiplying base by height, the area of the triangle will be half of that product. If the distance between two pegs of the geoplane in our drawing is 1 centimetre, the rectangle would have 3 × 6 = 18 cm² and then, the triangle will have half, exactly 9 cm².
By the way, for the drawing we have used this online geoplane, in case you want to use it for testing.
Area of a right triangle = (base × height) ⁄ 2
This formula is going to be useful to calculate the area also of non-right triangles, but if you want to know the reason, you will have to read the section about it.
How to Calculate the Area of a Rhomboid?
A rhomboid is a quadrilateral that has its sides parallel two by two. Like this one:
If you think about it, any paper rhomboid could be transformed, using scissors, by cutting a right triangle and moving it to the opposite end.
The result is a rectangle! So the rectangle and the rhomboid share the way of calculating the area, base times height.
Area of a rhomboid = base × height
How to Calculate the Area of a Triangle That Is Not a Right Triangle?
Both acute triangles and obtuse triangles can be seen as half rhomboids. If you copy and paste the triangle side by side, you can check it. Therefore, and as the area of the rhomboid is base times height, the area of these triangles -and of any triangle- is base times height by two:
Area of any triangle = (base × height) ⁄ 2
How to Calculate the Area of a Trapezoid?
A trapezoid is a quadrilateral that has two parallel sides, the two bases, like this one:
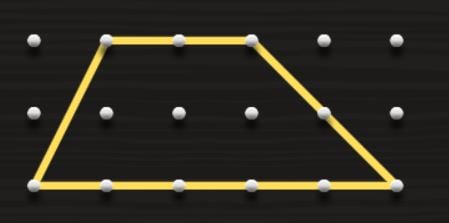
If you want to know the area of a trapezoid, the easiest thing to do is… the same we have done with the triangles! Just copy the trapezoid to the side and it becomes a rhomboid!
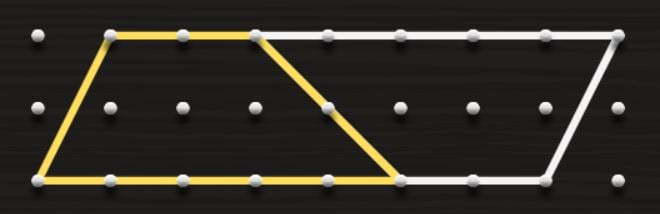
The base of this rhomboid is the sum of the trapezoid’s two bases, and the height stays the same. So, the area of the rhomboid would be (base 1 + base 2) × height and, as the trapezoid is half a rhomboid:
Area of a trapezoid = [(base 1 + base 2) × height] ⁄ 2
How to Calculate the Area of a Rhombus?
A rhombus is a quadrilateral that has four equal sides. By the way, squares have 4 equal sides. So, we can think squares as “limit cases” of rhombuses. But, for this entry, we are interested in a rhombus that looks something like this:
To calculate the area of a rhombus you need to know the length of its diagonals. We are going to call D the long diagonal and d the short diagonal (which are the vertical and horizontal line in the drawing, respectively).
In the image, you can already see a possible way to calculate the area of the rhombus. You can do it by calculating the area of the four identical triangles that are formed by the diagonals.
The area of any of these triangles will be base times height divided by two. Its base is half the d diagonal, and its height is half the D diagonal. Therefore, the area of one of these triangles is D times d divided by 8. And as we have 4 of these triangles, the area of the rhombus is:
Area of a rhombus = (D diagonal × d diagonal ) ⁄ 2
How to Calculate the Area of a Regular Polygon with More than 4 Sides?
A regular polygon has all its sides equal, also all its angles are equal. For example, look at the following heptagon, a regular polygon with 7 sides:
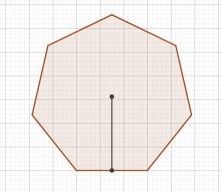
To calculate its area with primary or early secondary school tools, you need the length of its side (of any of them, they are ALL equal) and its apothem, which is the line that joins the center of the polygon with half of a side. In the heptagon we could draw 7 segments like this, but all of them would measure the same.
Notice what happens when you join a pair of consecutive vertices of the polygon with the center:
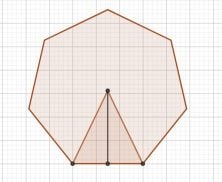
An isosceles triangle is formed (in the case of the hexagon it will be an equilateral triangle) that has as the base the side of the polygon and as the height the apothem of the polygon. The polygon is composed by as many triangles as the number of sides, in our case, 7.
The area of one of these triangles will be side times apothem divided by two. And, as we have 7 triangles, the total area will be 7 times side times apothem divided by two. But wait a minute, won’t 7 times the side be the perimeter of the whole polygon? That’s right! Then, we have a formula that does not require calculating each triangle and then multiplying by the number of triangles:
Area of a regular polygon = (perimeter × apothem) ⁄ 2
How to Calculate the Area of Any Non-regular or Compound Polygon?
As we saw at the beginning, if we are given a compound polygon, or a non-regular polygon, what we will have to do is look for parts of the polygon that we do know how to calculate, because we have enough data to do so.
Conclusion
As we have seen throughout this long entry, the calculation of areas is not only about learning formulas and applying them well, but also about reasoning and seeing that figures can be divided into simpler ones. Sometimes they will be sides, sometimes heights, sometimes diagonals…. But most likely they will be triangles. Triangles are the simplest polygons, and the key pieces of geometry.
Sign up at Smartick to try it for free. You will be able to practice exercises and problems of area calculation and other primary and secondary mathematics content adapted to your level.
Learn More:
- How to Calculate Perimeters: Part 1
- How to Calculate a Perimeter: Part 2
- Perimeter: What Is It and How to Find It for Any Polygon
- Calculating the Area of Polygons
- Learn the Properties of Geometrical Prisms
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.
- Mathematical Formulas: What Are They, How Are They Made and Types of Formulas? - 11/29/2024
- The Language of Functions and Graphs - 07/01/2024
- Educational Technology: The Christodoulou Test - 05/06/2024