How to Solve Double Digit Division

In today’s post we are going to explain how to solve double digit division.

Before beginning to learn how to solve double digit division, it is important that you become familiar with these terms, because we will use them later.

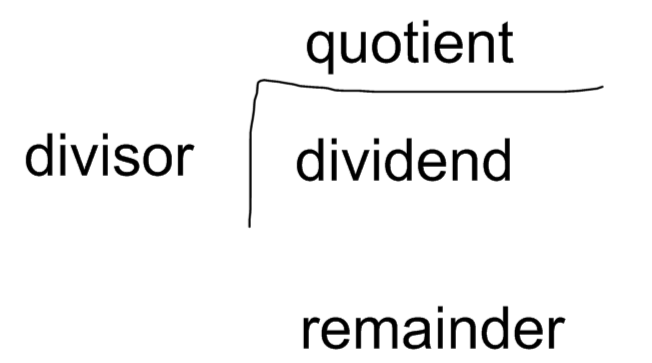
Dividend: the number that is being divided.

Divisor: the number by which the dividend is divided.

Quotient: the result of division.

Remainder: the amount that is left over after division.

Once you have seen this, you know where to place each number in the division. Now, we have to follow these steps:

1. Take the first digits of the dividend, the same number of digits that the divisor has. If the number taken from the dividend is smaller than the divisor, you need to take the next digit of the dividend.
2. Divide the first number of the dividend (or the two first numbers if the previous step took another digit) by the first digit of the divisor. Write the result of this division in the space of the quotient.
3. Multiply the digit of the quotient by the divisor, write the result beneath the dividend and subtract it. If you cannot, because the dividend is smaller, you will have to choose a smaller number in the quotient until it can subtract.
4. After subtraction, drop the next digit of the dividend and repeat from step 2 until there are no more remaining numbers in the dividend.

That’s the concept, but we are going to go through it with an example.

We are going to solve the following double digit division:

1. Take the first digits of the dividend: in this case 57. But as 57 is smaller than 73, you have to take one more digit: 573.

2. To divide 573 by 73, we take the first two digits of the dividend: 57 and divide them by the first digit of the divisor:

57 ÷ 7 = 8

3. Write the 8 in the quotient and multiply it by the divisor:

8 x 73 = 584

But 584 is bigger than 573; therefore, 8 “does not fit”. You have to choose the preceding number and multiply again:

7 x 73 = 511

511 is smaller than the dividend; therefore 7 “does fit”. We write 511 beneath the digits of the dividend and then divide and subtract:

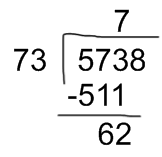
4. Drop the next digit of the dividend, which is 8. Now, you have to divide 628 by 73. Repeat the previous steps:

Divide the first two digits of the dividend by the first digit of the divisor and write it in the space of the quotient:

62 ÷ 7 = 8

Multiply that digit by the divisor:

8 x 73 = 584

584 is less than 628; therefore, we can subtract:

628 – 584 = 44

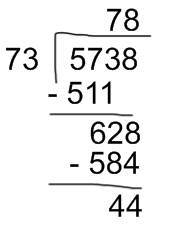
The result of this division is 78 and a remainder of 44.

I hope that you have learned with this post how to do double-digit division.

Do not hesitate to leave your comments!

And if you want to learn more math, sign in Smartick

Learn More:

• How to Solve a Problem Involving Dividing 2 Digit Numbers
• How to Do 2 and 3 Digit Division
• Practice 3-Digit Division Examples
• Learn How to Do Single Digit Division
• Learn How to Do a 3-Digit Division Problem

Fun is our brain’s favorite way of learning

Diane Ackerman

Smartick is a fun way to learn math

• 15 fun minutes a day
• Adapts to your child’s level
• Millions of students since 2009

Start your 7-day free trial

• Author
• Recent Posts

Smartick

Content Creation Team.
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.

Latest posts by Smartick (see all)

• The Language of Functions and Graphs - 07/01/2024
• Educational Technology: The Christodoulou Test - 05/06/2024
• Multiplication Activities in Smartick - 04/09/2024