In today’s post we will look at how to calculate the square of the sum of two numbers a and b, (a + b) ².
Notable Identities:
For example: We built a square with sides of a + b units length:
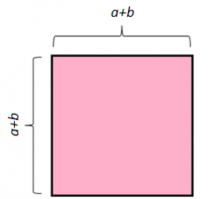
If we calculate the area of this square (we know that the area of a square is side multiplied by side), it gives us: (a + b)(a + b), which would be the same as (a + b) ² square units.
Then we will divide the square into four parts:
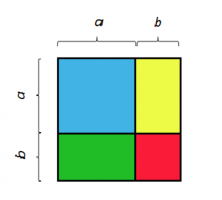
Now, we have two squares (blue and red) and two rectangles (green and yellow). We calculate the areas of each figure:
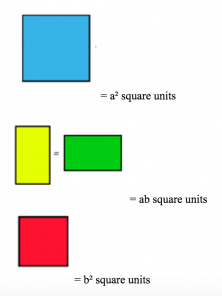
It is easy to see that the area of the first pink square of side a + b, is the sum of the areas of the blue square (= a²), of the red (= b ²) and the two equal yellow and green rectangles (= 2ab)
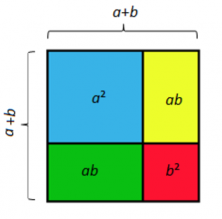
Therefore, we can see that (a + b) ² = a² + 2ab + b ².
There are several identities of great importance in mathematics that must be learned to be handled with ease:
(a+b) ² = a² + 2ab + b ²
(a-b) ² = a² – 2ab + b ²
(a+b)(a-b) = a² – b²
Often they lead us to make mistakes when doing calculations with them, so it is important not to simply memorize formulas but try to see where they come from.
We have just seen, from the geometric point of view, how to square the sum of two quantities (in our case a and b).
I hope you liked this post and that it has helped you understand the notable identities a little more. We can do the same with squaring the difference of the two numbers and multiplying the sum by the difference. Try to do it yourself, I am sure it will come out well!
Remember that at Smartick you can practice identity exercises, and much more!
Learn More:
- Distributive Property in Geometry
- How to Perform Multiplication Problems with an Area Model
- Learn about the Distributive Property of Multiplication
- Let’s Learn about Ratios with Singaporean Bar Models
- Calculating the Area of Polygons
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.
- The Language of Functions and Graphs - 07/01/2024
- Educational Technology: The Christodoulou Test - 05/06/2024
- Multiplication Activities in Smartick - 04/09/2024