In today’s post, we’re going to take a look at some strategies for solving problems that involve incomplete horizontal additions and subtractions, using examples to help us.
Acquiring mental calculation strategies is not always easy, since there’s no defined “best method” for everyone, and it can be frustrating if you don’t pick it up quickly.
Be patient, little by little you’ll add more strategies to your list until it’s full!
Example of how to solve incomplete horizontal additions
First of all, let’s take a look at how to solve the following incomplete addition:
When we see the “+” symbol and two numbers, the first thing you might think is that you have to add. Don’t get confused! What you need to do is look for a number that, added to 86, gives a result of 756.
Since the inverse operation of addition is subtraction, the number we’re looking for will be the result of subtracting 86 from 756.
You can perform this subtraction by breaking down the two numbers in the way that is easiest for you. I’ll show you how I do it:
- Since 756 and 86 have the same quantity of units, first I break down 86 into 80 and 6. Then I subtract the 6 (which is the easiest to start with) and finally, 80:
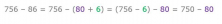
- Now, since 750 has 5 tens, I separate the 80 into 50 and 30 to make it easier to subtract. I subtract the 50 and then the 30:
We’ve found the number we were looking for!
756 – 86 = 670, therefore, 670 + 86 = 756. So the number we need to fill the gap is 670.
Example of how to solve an incomplete horizontal subtraction
Now let’s see how to solve the following incomplete subtraction:
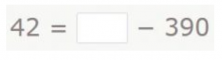
Just like before, when we see the “-” symbol and two numbers, the first thing you might think is that you have to subtract. But if you look carefully, you’ll see that what you need to do is look for a number that, when subtracted from 390, gives a result of 42.
Since the inverse operation of subtraction is addition, the number we’re looking for will be the result of adding 390 and 42.
Once again, you can perform this addition by breaking down the two numbers in the way that is easiest for you. Here’s how I do it:
- First I add the units, which are the easiest to add. So, in this case, I break down the 42 into 40 and 2 and add:
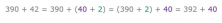
- Since 392 has 9 tens, it needs 1 more ten to form another hundred. So I break down the 40 into 10 and 30. Now I can add the 10 and then the 30:
- This addition is very simple, since none of the units, tens or hundreds in either number match:
We’ve found the number we were looking for.
390 + 42 = 432, therefore, 432 – 390 = 42, so the number that we need to fill the gap is 432.
See how easy it is to solve problems involving incomplete horizontal additions and subtractions?
But remember: Before applying these strategies, you first need to look and think.
Now try solving the following incomplete subtraction, which is a bit different from the previous ones. You can leave your answer in the comments:
And if you want to practice these types of exercises and other primary mathematics, register with Smartick and try it for free.
Learn More:
- Incomplete Horizontal Addition and Subtraction to Develop Mathematical Flexibility
- Mental Calculation: Horizontal Addition and Subtraction
- Completing Additions, Subtractions, Multiplications and Divisions
- How to Solve a Subtraction Problem with Regrouping
- Subtraction With and Without Carrying
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.
- The Language of Functions and Graphs - 07/01/2024
- Educational Technology: The Christodoulou Test - 05/06/2024
- Multiplication Activities in Smartick - 04/09/2024