The order of operations is a fundamental concept in mathematics for solving numerical expressions effectively. Understanding and applying the order of operations is very important in order to solve mathematical operations correctly, avoid common mistakes and ensure accurate results. It is essential for the understanding and the solution of algebraic expressions and equations correctly.
Index
What Is the Order of Operations?
The order of operations is the rule that establishes the order in which mathematical operations should be performed when several operations appear in the same expression, something that is often also called combined operations. The order of operations ensures that operations are performed in the correct order to obtain the expected result.
What Is Pemdas and What Does It Have to Do with the Order of Operations?
The order of operations is often simplified by the rule “PEMDAS”. It is a word formed from the initials of:
- Parentheses
- Exponents (powers)
- Multiplication
- Division
- Addition (addition)
- Subtraction (subtraction)
PEMDAS acts as a guide to highlight the order in which you should solve the operations within a mathematical expression.
So, first you will have to solve what is in parentheses, then the exponents, then the multiplication and division, and finally any addition and subtraction.
Risks of Using Pemdas When Solving Order of Operation Problems
In mathematics, we are sometimes many tips and tricks. Could PEMDAS be the solution to all combined operations problems? We don’t think so, for several reasons:
- As we already explained in the post dedicated to combined operations, if there are no parentheses, but there are multiplications and divisions, or additions and subtractions, you have to do them in the order they appear from left to right. In other words, multiplication and division, on the one hand, and addition and subtraction, on the other, have the same priority. That is, if you find one or the other in the expression and there is no other operation with a higher priority, you solve them from left to right. This is a risk, because when reading PEMDAS (and memorizing “parentheses, exponents, multiplications and divisions, additions and subtractions”) you may forget the “ands” that appear and think that multiplications have priority over divisions or that additions have priority over subtractions, which is not the case.
- Perhaps, in the combined operation you have to solve, a symbol or operation appears that is not mentioned in the list, for example, a square root, occupies the same place as the exponents, or a square bracket, [], or curly bracket, {}, which mean the same as the parentheses, although not mentioned.
- Another risk when learning a mnemonic rule such as PEMDAS is to confuse some letters, thinking, for example, that the P at the beginning is for “powers”, when it is for parentheses.
- Inside a parenthesis there could be another combined operation, in which case I would again apply the rule of the order of operations, and you would have to solve first the parentheses inside the parenthesis, then the exponents, then the multiplication and division, and finally the addition and subtraction.
The conclusion is that instead of just following a rule that gives very few explanations and leaves operations unmentioned, when you are faced with a combined operation, start by solving the parentheses (and square brackets or curly brackets that may be present), continue with any powers and roots, then apply the multiplication and division (from left to right) and then the addition and subtraction (also from left to right).
The Order of Operations Is Compatible with Other Rules of Mathematics
Sometimes it is better to use other rules of mathematics (such as the commutative or distributive properties) instead of going directly to the order of operations, see:
Following the order of operations we would have to solve the parenthesis first, but if we use the distributive property we will have:
Now, in the order of operations, we first perform the divisions:
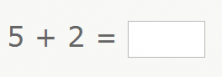
And we added, obtaining the same result, without having to do the addition at the beginning, which was not difficult either, because it gives 63.
The image we used to illustrate this post also has a “trick” in mathematics that can save you from calculating a three-digit number, can you guess what it is? Leave your solution in the comments.
Video Tutorial on the Order of Operations
To continue learning about the order of operations, you can watch our video tutorial on order of operations. But the best thing to do is to register with Smartick and do your sessions, it only takes 15 minutes. This way, with practice, you will end up mastering the order of operations and many other mathematical questions.
Learn More:
- Learn How to Perform Combined Operations
- Combined Operations: How to Solve These Types of Problems
- What Are Combined Operations?
- Tricks to Solve Combined Operations
- How to Solve Combined Operations
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.
- Mathematical Formulas: What Are They, How Are They Made and Types of Formulas? - 11/29/2024
- The Language of Functions and Graphs - 07/01/2024
- Educational Technology: The Christodoulou Test - 05/06/2024