In today’s post, we are going to learn about the different methods we can use to simplify fractions, as well as a trick that is essential to simplification. We will also see some examples of activities that children solve during their Smartick sessions.
Index
What is Simplifying Fractions?
Simplifying a fraction is reducing the numerator and denominator to another fraction with smaller numbers. The fraction we are left with is equivalent to the initial fraction and therefore represents the same quantity just represented differently.
For example: let’s look at the case of the fraction four eighths.
The bar is going to help us see the fraction. It is divided into 8 parts and 4 have been colored. A simple look and we can see that this represents half of the bar, in other words, four-eighths is equivalent to one half. But it is not just this, one four eighths is equivalent to an infinite amount of fractions.
In this case, I am going to ask you to take note of the two fractions on the right, they have something in common. They represent the same quantity as four eighths, but with fewer parts:
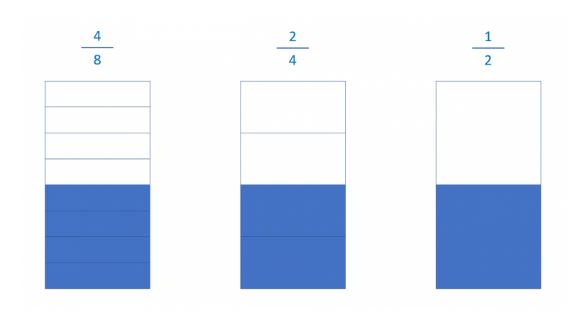
All of the fractions represent the same quantity with different amounts in the numerator and denominator, they are equivalent fractions to one another.
They are simplified fractions of another fraction that, along with the previous example, represent the same amount that the original fraction did but with fewer parts.
In other words, \(\frac{2}{4}\) and \(\frac{1}{2}\) are simplified fractions of \(\frac{4}{8}\)
In order to simplify a fraction, you need to divide the numerator and denominator by the same number.
We call this process reducing a fraction.
First, we will try it with prime numbers (2, 3, 5, 7, 11…), reducing by dividing by 2.
For example \(\frac{24}{30}\)
- If we divide the numerator and denominator by 2 we are left with \(\frac{12}{15}\).
- Now we will do the same and reduce the fraction \(\frac{12}{15}\) by dividing the two terms by 3 because we cannot divide them by 2. Remember we need to divide the numerator and denominator by the same number. We are left with \(\frac{4}{5}\). This fraction is equivalent to the previous fractions.
- \(\frac{4}{5}\) cannot be reduced because there is no number – aside from one – that is a divisor for 4 and 5. The fraction we are left with is called an irreducible fraction because it cannot be simplified.
Video: How to Simplify Fractions
To better understand how to simplify fractions, take a look at the following video. It is a video of one of our interactive tutorials and although it is not interactive in this format, you are able to watch it as many times as necessary and share it with friends. If you would like to access our interactive tutorials, register with Smartick! The online method which helps children ages 4 to 14 learn and practice math.
How to Simplify Fractions
There are two methods to simplify fractions which we will explain below. Then you can choose which one you prefer to use when simplifying fractions.
Method 1 to Simplify Fractions: Common Divisor
For this method, we need to divide the numerator and denominator by a common divisor until there are no more common divisors.
Let’s look at an example.
At a game between the Blue Owls and Red Cats there were 120 spectators – 80 supporting the Owls and 40 supporting the Cats. What fraction of the spectators were cheering for the blue team?
Otto and Eva want to know what the irreducible fractions are for the supporters of each team. As you can see, the fractions they currently have consist of large numbers.
We are going to find the irreducible fraction of the Blue Owl fans \(\frac{80}{120}\).
Since the numerator and denominator are both even numbers, they can be divided by 2. We are left with \(\frac{40}{60}\).
Since 40 and 60 are multiples of 2, we can divide them by this again and are left with \(\frac{20}{30}\).
We can also divide 20 and 30 by 2, and will have the fraction \(\frac{10}{15}\).
As you can see, \(\frac{10}{15}\) cannot be reduced by dividing its terms by 2, but they can be divided by 5 that leaves us with \(\frac{2}{3}\). This is an irreducible fraction because there is no common divisor between the numerator and denominator besides 1.
Maybe this method seems a bit tricky. Keep reading to see another way to simplify fractions that is quicker and easier.
Method 2 to Simplify Fractions: GCD
In the second method, we need to divide the numerator and denominator by their greatest common divisor (GCD).
You could see it coming! We need to look for common divisors of the numerator and denominator, so why not divide it by the largest of the common divisors and finish sooner?
We are going to see how we can reduce fractions using this method with the previous Blue Owls example.
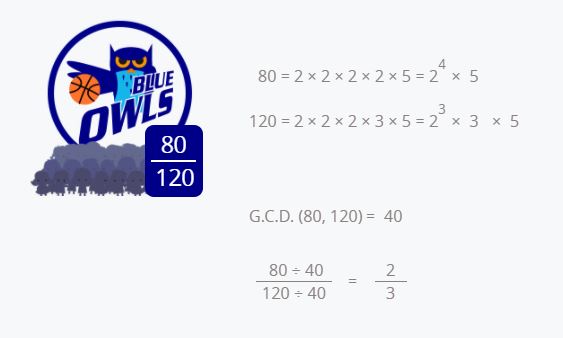
We calculate the maximum common divisor of 80 and 120.
As shown in the image above we take the common divisors of 80 and 120, which are 2 and 5, and in both cases, we choose the smaller exponent.
The factor 2, the smaller exponent is 2³ and the factor 5, the smaller exponent is 5¹.
Therefore 2³ × 5 = 40 is the most common divisor.
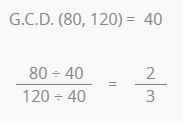
So we divide the numerator and denominator by 40.
\(\frac{2}{3}\) is the irreducible fraction of \(\frac{80}{120}\).
Video to Learn How to Simplify Fractions Using the GCD
You can also take a look at this video where Otto and Eva go to a basketball game for their favorites teams and use the process of simplifying fractions that we just explained.
Trick For Simplifying Large Fractions
Pay attention! This trick is very good for simplifying fractions that have large numbers.
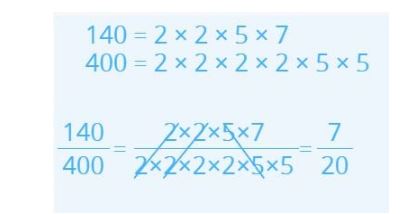
- As shown in the image, we break down the numerator (140) and the denominator (140) into prime factors and write the factors of each in the form of a fraction.
- We cross out the factors that are the same, both in the numerator and denominator, and multiply the factors that were not crossed out.
- In the numerator, we only have 7 and in the denominator, we have 2 × 2 × 5 which is 20.
- Finally, we are left with \(\frac{7}{20}\) which is the irreducible fraction of \(\frac{140}{400}\).
Be very careful when using this method. We can only cross out common factors, the numbers that can be multiplied to get the numerator and denominator.
Examples of Simplifying Fractions
To keep learning, we are going to look at a few examples of activities that children complete during their Smartick sessions when learning to simplify fractions.
Activity 1
In this activity, you first need to mentally calculate the simplified fraction in order to find out which is the correct answer.
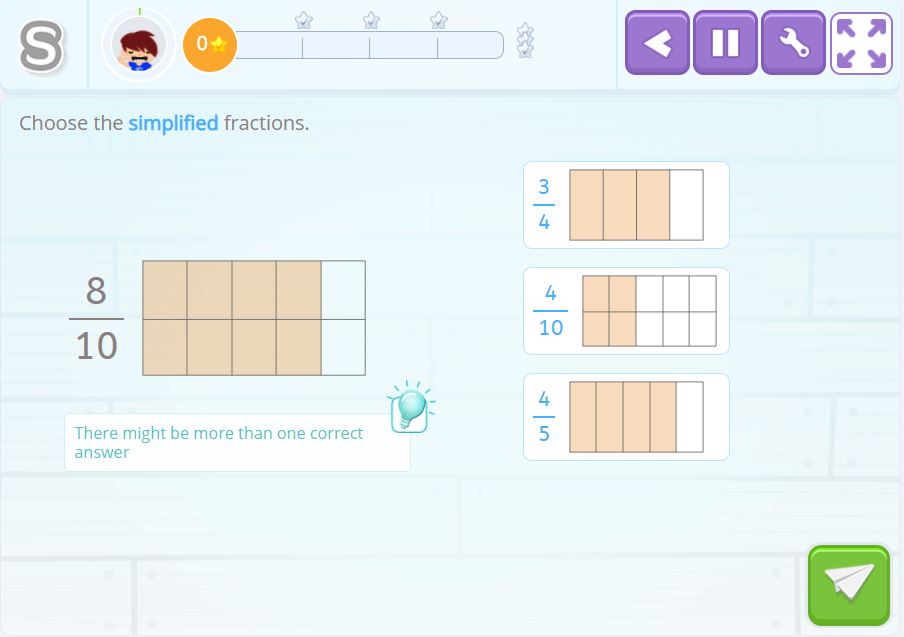
Solution 1
If we mentally eliminate the horizontal line, we see that the simplified fraction of \(\frac{8}{10}\) is \(\frac{4}{5}\).
Activity 2
We want to find the simplified fraction to represent the gray stars. By counting the gray stars from the total number of stars we see that the fraction, before simplification, is \(\frac{3}{15}\).
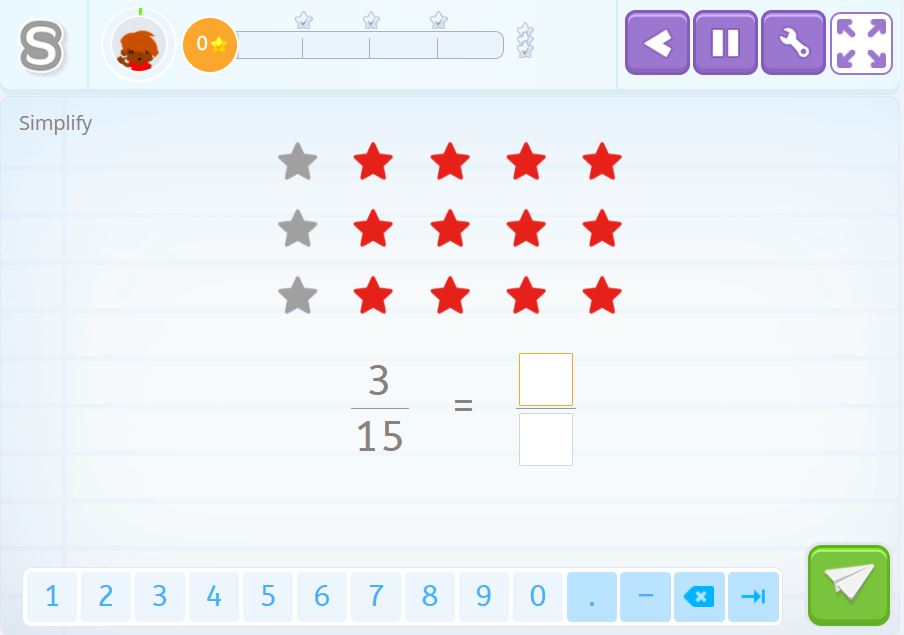
Solution 2
Looking at how the stars are organized into columns, we see that one of the five columns is gray. Therefore the simplified fraction of \(\frac{3}{15}\) is \(\frac{1}{5}\).
Activity 3
You already know that you can use the two different methods that we previously explained to simplify the fraction, whichever method you prefer.
And if you have a fraction with larger numbers, remember to use the trick that we have shown you.
Solution 3
For both of the methods we have shown, the solution would be \(\frac{2}{5}\).
Activity 4
In this activity, we divide by different numbers until we find an irreducible fraction.
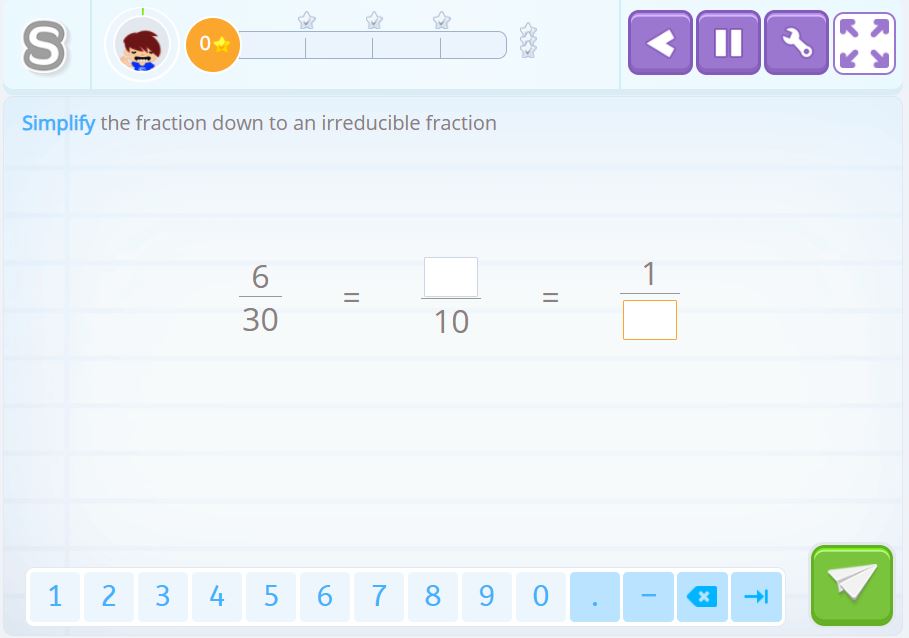
Solution 4
We divided the numerator and denominator by 3 and obtained \(\frac{2}{10}\) which is not irreducible. Then by 2 which resulted in \(\frac{1}{5}\), which is the irreducible fractions because there is no other number that we can divide the numerator and denominator by.
Activity 5
In this activity, you need to take out the equivalent fractions and can use the images to help you.
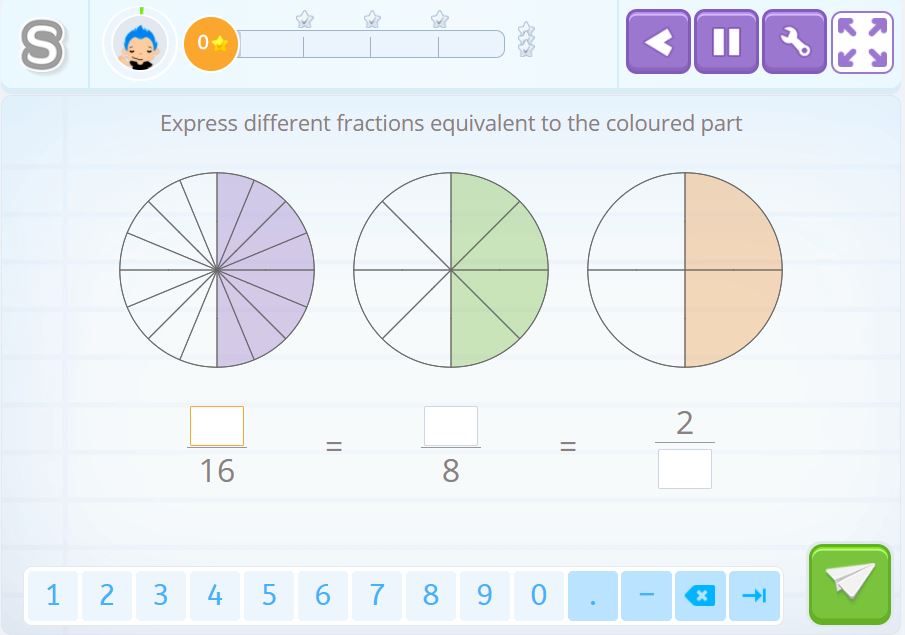
Solution 5
Observing the colored parts, we see that the first numerator needs to be 8 and the second, 4. Looking at how the third is divided, we see that the denominator is 4. We have simplified the fractions, obtaining equivalent fractions, but not finding an irreducible fraction, which is \(\frac{1}{2}\).
Activity 6
You need to write a simplified fraction with help from the number line.
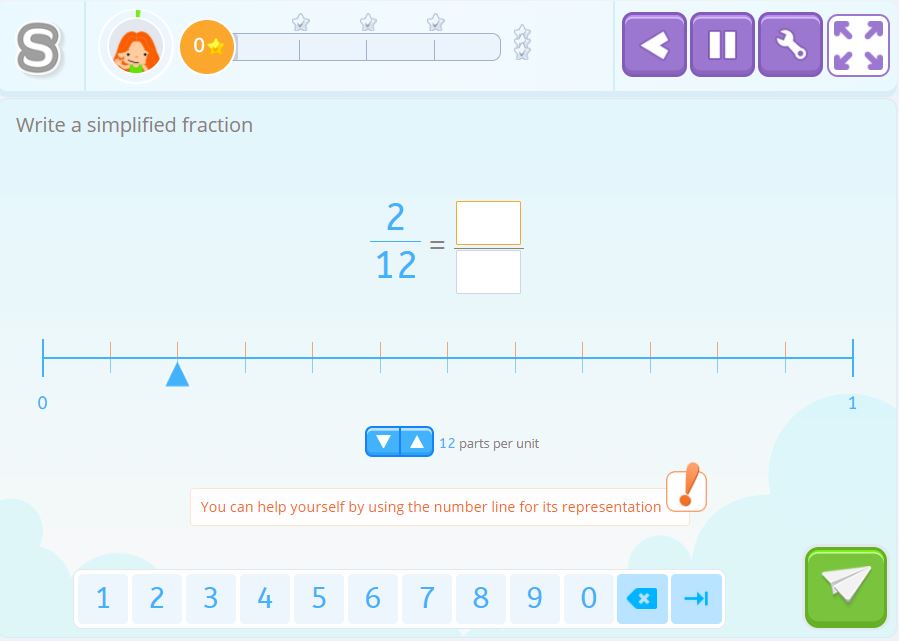
Solution 6
This visual support used in this activity is a number line.
\(\frac{2}{6}\) corresponds to dividing the length of a segment into six equal parts and then staying at the second mark. Since the simplified fraction is \(\frac{1}{3}\) we could have also divided the length into three parts and then stayed at the first mark.
If you have enjoyed this post and would like to learn more about how to simplify fractions and other math topics, register with Smartick and try it for free!
Learn More:
- Subtracting Fractions Exercises with Common and Uncommon Denominators
- Learn and Practice How to Subtract or Add Fractions
- Types of Fractions: Proper, Improper, Fractions Equal to One
- Two Ways of Dividing Fractions and Some Examples
- Review and Practice the Two Methods of Dividing Fractions
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.