In today’s post, we are going to explain exercises with subtracting fractions. We will also see some of the Smartick activities about subtracting fractions that children complete during their sessions.
In an earlier blog post, we explained how to subtract fractions. You can take a look and review this post before reading more.
In order to subtract fractions, we need to know how to calculate the Least Common Multiple between different numbers.
If you already know how to find the Least Common Multiple of numbers let’s continue!
Index
Subtracting Fractions with Common Denominators
Steps to Subtract Fractions with Common Denominators
We can subtract fractions without any extra steps when they have a common denominator, you just need to:
- Write the common denominator from the fractions in the result.
- Subtract the numbers in the numerator and write the result in the numerator of the result.
Examples
- \(\frac{7}{3}\) – \(\frac{2}{3}\) = \(\frac{5}{3}\)
- \(\frac{10}{5}\) – \(\frac{2}{5}\) = \(\frac{8}{5}\)
Solved Exercises
Now we are going to see a few activities that children solve during their Smartick sessions about subtracting fractions with common denominators.
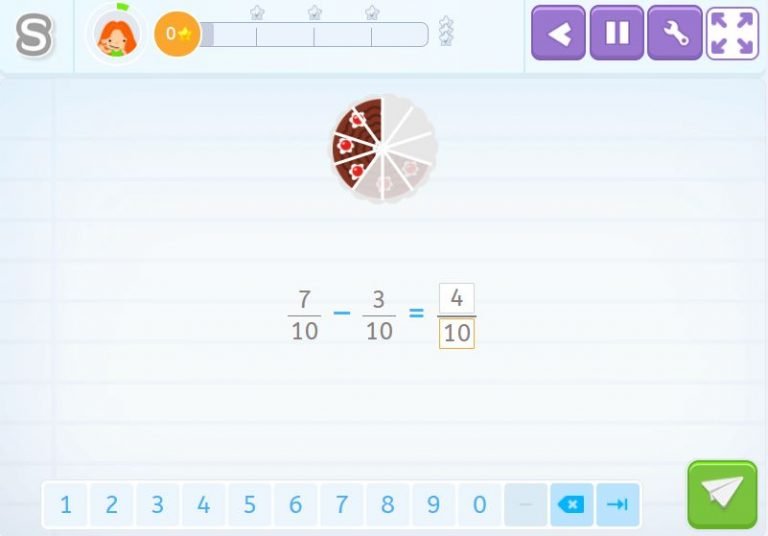
As you can see, the cake is a visual representation that helps you subtract fractions. It is divided into 10 equal parts, which in the end we are left with 4 pieces of cake.
\(\frac{7}{10}\) – \(\frac{3}{10}\) = \(\frac{4}{10}\) pieces of cake.
Since the first fraction, \(\frac{4}{10}\), has an even numerator and denominator, it can be simplified which will give you \(\frac{2}{5}\) of cake even if the pieces have been cut and cannot be put back together.
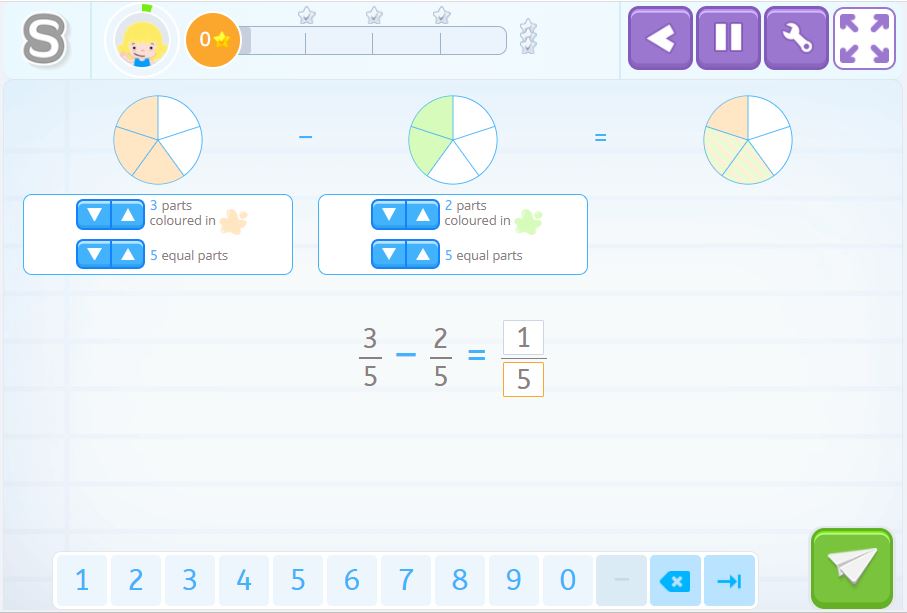
In this activity, you use circles to help you represent the fractions. First, we need to divide the two circles into 5 equal parts and then we need to color in 3 parts of one circle, and 2 parts of the other. We can see that the result is a circle that only has one orange part.
\(\frac{3}{5}\) – \(\frac{2}{5}\) = \(\frac{1}{5}\) colored parts of the circle.
Subtracting Fractions with Uncommon Denominators
We can find them:
- Subtracting more complex fractions. These types of fractions are those that have uncommon denominators that are not multiples of one another. For example: \(\frac{5}{6}\) – \(\frac{7}{13}\)
- Subtracting more simple fractions. These types of fractions are those that have uncommon denominators, and the denominators are multiples of one another. For example: \(\frac{5}{6}\) – \(\frac{7}{12}\) (12 is a multiple of 6).
In both cases, we have to create fractions with common denominators so that we can complete the subtraction.
Steps to Subtract Complex Fractions with Uncommon Denominators
To subtract more complex fractions, we have to have fractions that have a common denominator, and this denominator should be a multiple of the two current denominators. It can be any common multiple, but we would recommend using the least common multiple:
- Find the least common multiple of the denominators.
- Write the new fractions, which are equivalent to the initial fractions, with the least common multiple as the denominator.
- The resulting fractions will have a common denominator so we can proceed as we did with the previous example: subtracting the numerators and writing their result as the numerator of the resulting fraction.
Example 1
\(\frac{2}{3}\) – \(\frac{3}{5}\)
The first thing we are going to do is find the least common multiple between the denominators of the fractions:
l.c.m. (3, 5) = 15
Now we will write the equivalent fractions of the previous fractions with a denominator of 15:
\(\frac{2}{3}\) = \(\frac{?}{15}\)
In order to find the numerator, we need to multiply it (2) by the same number we used to get the denominator.
To get from 3 to 15 we multiplied by 5. This is why we will also multiply the numerator by 5.
\(\frac{2}{3}\) = \(\frac{10}{15}\)
We will do the same with the other fraction:
\(\frac{3}{5}\) = \(\frac{?}{15}\)
The denominator was multiplied by 3 so the numerator will also be multiplied by 3:
\(\frac{3}{5}\) = \(\frac{9}{15}\)
Now that the fractions have the same denominator we can subtract:
\(\frac{10}{15}\) – \(\frac{9}{15}\) = \(\frac{1}{15}\)
Example 2
\(\frac{5}{6}\) – \(\frac{3}{10}\)
The least common multiple between 6 and 10 is 30.
We found the equivalent fractions:
\(\frac{5}{6}\) = \(\frac{?}{30}\)
The denominator was multiplied by 5 so the numerator will also have to be multiplied by 5:
\(\frac{5}{6}\) = \(\frac{25}{30}\)
Now we do the other fraction:
\(\frac{3}{10}\) = \(\frac{?}{30}\)
The denominator was multiplied by 3, so the numerator also needs to be multiplied by 3:
\(\frac{3}{10}\) = \(\frac{9}{30}\)
Finally we subtract the fractions:
\(\frac{25}{30}\) – \(\frac{9}{30}\) = \(\frac{16}{30}\)
The last fraction can also be simplified:
\(\frac{16}{30}\) = \(\frac{8}{15}\)
Steps to Subtract Simple Fractions with Uncommon Denominators
We could find the least common multiple between the denominators but we are going to see another way of subtracting more simple fractions, just for these types of fractions:
- Find the equivalent fraction of the fraction that has a denominator that is a divisor of the other fraction so that the denominators of the two fractions are equal.
- The resulting fractions already have the same denominator so we subtract the numerators and write the resulting fraction.
Example 1
\(\frac{5}{6}\) – \(\frac{7}{12}\)
The equivalent fraction to \(\frac{5}{6}\) is \(\frac{10}{12}\), we have multiplied the numerator and denominator by 2.
Now we have two fractions with the same denominator, 12:
\(\frac{10}{12}\) – \(\frac{7}{12}\)
So the result of the subtraction is:
\(\frac{10}{12}\) – \(\frac{7}{12}\) = \(\frac{3}{12}\)
Example 2
We can also look for this equivalent fraction visually and intuitively. Let’s look at several examples of Smartick activities.
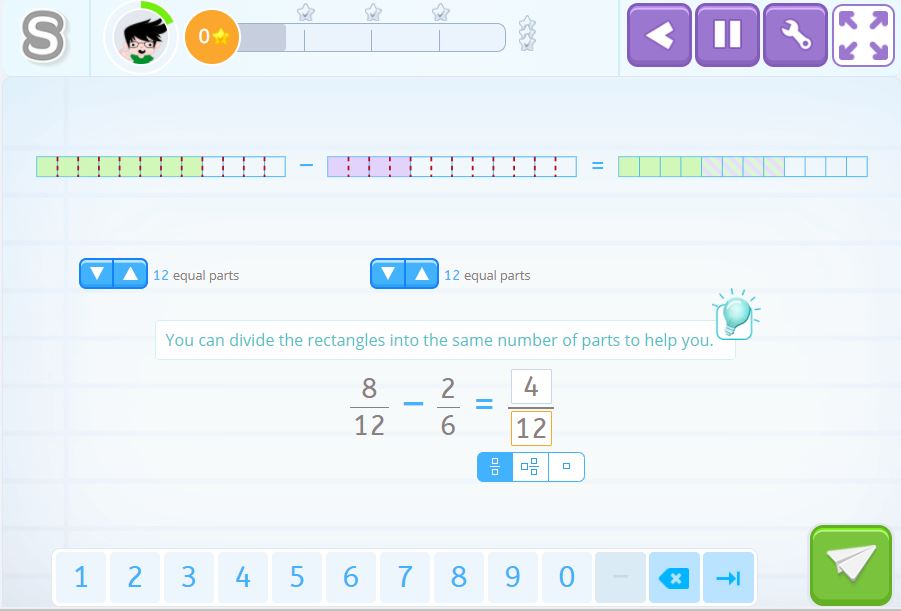
To solve this activity we need to do two things:
- Find the l.c.m of 12 and 6, which is 12.
- Create equivalent fractions as we have seen in previous examples.
In this activity you can use the bars to help you find the result of the fraction simply by representing the same number of parts on the two bars, in this case, they would be divided into 12 equal parts.
Once we have the same denominator for the two fractions we can subtract and you already know that for the fractions to have common denominators we need to find the l.c.m or find equivalent fractions. I have already done it for you:
\(\frac{8}{12}\) – \(\frac{2}{6}\) = \(\frac{4}{12}\), as you can see, that is already represented by the bar, there are only four colored squares and the bar is divided into 12 parts.
Solved Exercises
And finally, we are going to look at some examples of activities that children can do in Smartick to practice subtracting fractions with uncommon denominators.
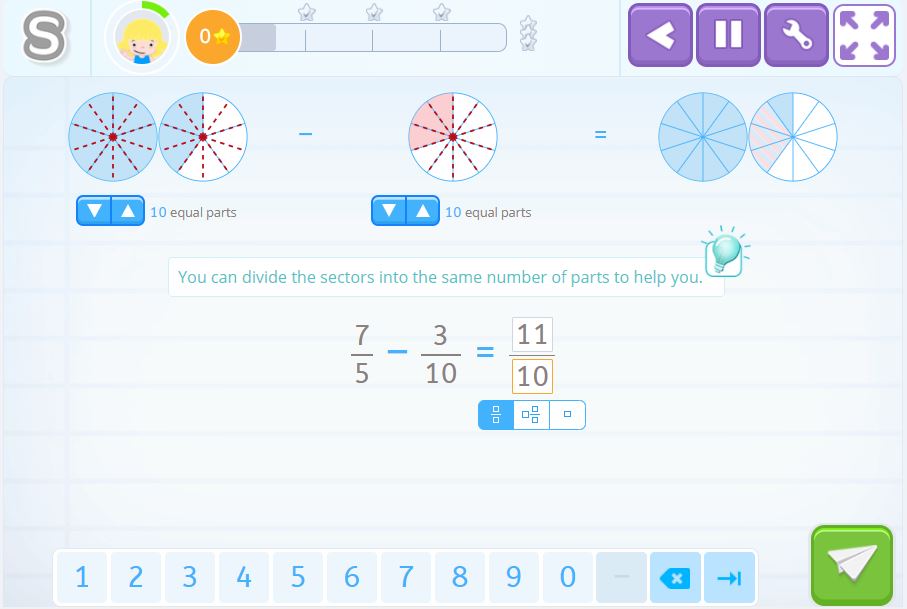
This activity is the same as the previous only this time we are using circles to represent fractions.
You can use the circles to show the result of the fraction, you simply need to put the same number of parts in both circles which in this case is 10.
As you can see, the result of subtracting the fractions is \(\frac{11}{10}\). You can check if you have done it correctly by looking at the result of the circles. One complete circle, and one colored part.
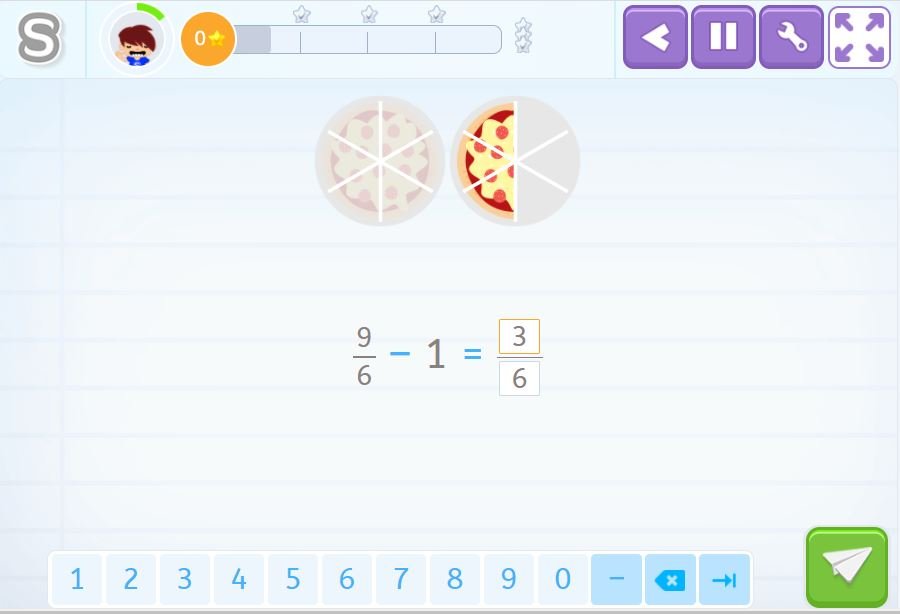
This activity is very easy, here the pizzas can help us figure out the result of subtracting fractions.
You already know that you have two options to solve an exercise:
- Find the l.c.m of 6 and 1, which is 6.
- Create equivalent fractions as we have seen in previous examples.
Have you learned how to subtract fractions?
Now I will give you the following exercises to practice what you have learned.
- \(\frac{8}{5}\) – \(\frac{3}{5}\)
- \(\frac{3}{2}\) – \(\frac{2}{3}\)
- \(\frac{7}{4}\) – \(\frac{7}{8}\)
- \(\frac{5}{6}\) – \(\frac{1}{15}\)
The solutions are:
- \(\frac{5}{5}=1\)
- \(\frac{5}{6}\)
- \(\frac{7}{8}\)
- \(\frac{23}{30}\)
Video to Understand Equivalent Fractions
The following video is to help you better understand equivalent fractions to help you subtracting fractions with uncommon denominators.
This is a video of one of our interactive tutorials and although it is no longer interactive, you have the advantage of watching it as many times as you need and are able to share it with friends. If you would like to access our interactive tutorials, register with Smartick! The online method which helps children ages 4 to 14 learn and practice math.
And if you want to keep learning about subtracting fractions and other elementary math topics adapted to your level, register with Smartick and try it for free.
Learn More:
- Learn How to Subtract Fractions
- Learn and Practice How to Subtract or Add Fractions
- Learning How to Subtract Fractions
- How to Find a Sum of Fractions
- Learn and Practice How to Find Sums of Fractions
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.
- The Language of Functions and Graphs - 07/01/2024
- Educational Technology: The Christodoulou Test - 05/06/2024
- Multiplication Activities in Smartick - 04/09/2024