In this post, we are going to learn quite a few things about probability: what it is, what it’s used for, and how it is calculated, as well as some examples that we could find in our daily life.
Index
What is Probability?
One of the most special characteristics humans possess that sets us apart from other species is our ability to ‘predict’, to anticipate events that are going to happen. Sometimes we fail, but many other times we don’t. This capability has allowed us to get to where we are today, being able to predict both dangers and opportunities. Think about it, our ancestors who were able to predict a predator attack were the ones who survived. Now, tens of thousands of years later we’ve taken it a step further and wonder, what is probability?
Probability is the mathematical calculation that evaluates the possibilities that exist for an event to happen when chance intervenes.
Let’s look at a few examples because probability – like so many concepts in mathematics – is an abstract construct that is better understood with examples.
If you spin the wheel, what numbers could you land on?
The spinning wheel can stop at any number from one to five. Without realizing it, we have built an experiment (spinning the wheel) and the sample space (the numbers 1 to 5). A sample space is a set that has the possible outcomes, that is, the numbers one to five.
From our experience with board games, we already know more about the previous experiment. It is possible that the spinning wheel may stop on one of those numbers and it is impossible, for example, for it to land on an eight. We know quite a lot about probability and did not even realize it!
Let’s look at another experiment in a different context:
Looking at this parking lot, if a car leaves the lot what color could it be?
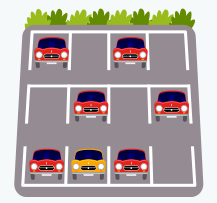
The possibilities are very clear, either a red car or yellow car can leave the parking lot. It is impossible for a green car or blue moped to leave. Even though there is the possibility of a yellow car leaving, it is more probable that a red car will because there are more red cars than yellow ones.
How to Calculate Probability
To calculate probability we will continue with the previous example and it is nothing more than counting how many cars there are of each color. Since 6 of the 7 cars in the parking lot are red, we can write it as a fraction: the probability of a red car leaving the parking lot would be a fraction with a numerator of 6 (the number of red cars) and a denominator of 7 (the total number of cars).
The probability of a red car leaving is equal to \(\frac{6}{7}\). The probability of a yellow car leaving is equal to \(\frac{1}{7}\). The probability of a blue car leaving would be 0 because there are no blue cars in the parking lot.
Generalizing this idea we come to how probability is calculated: with a fraction that is often called the Laplace rule. We put the number of favorable cases in the numerator, and we put the number of possible cases in the denominator.
We can now calculate probabilities of very simple events, for example, we can make predictions of the balls that will come out of this raffle drum:
There are 8 balls in the raffle drum:
- The probability that one will come out is \(\frac{1}{8}\)
- But four balls are the same and have the number 5, so the probability that a 5 will come out is \(\frac{4}{8}\). If you’re asked to bet on any results, the most likely is 5.
Mathematicians see the benefits that can be obtained from these predictions and have really developed this field. We at Smartick have done so as well with a sequence of exercises sorted by level which adapt to the learning pace of each child.
Example: Tossing a Coin
If you toss a coin, the probability that it lands on heads is \(\frac{1}{2}\), the same goes for it landing on tails.
Example: Rolling Dice
If you roll a die the probability that it will land on three would be \(\frac{1}{6}\).
You can also calculate the probability of it landing on an even number. Since there are three sides that have even numbers (2, 4, & 6) and six sides in total it would be, \(\frac{3}{6}\)=\(\frac{1}{2}\)
Why do We Use Probability?
Probability is used in many areas, such as mathematics, statistics, physics, economics, and social sciences among others. The first probability studies were developed to solve gambling problems and that’s where its use is most noticeable because it can help you have more chances to win, or to save, money (by choosing not to play in games you’re more likely to lose in).
Example: Odds and Evens
Look at the following example using the children’s game Odds and Evens.
Odds and Evens is a game that is used to choose between two people. Two people choose between odd or even, and at the same time show the number of fingers that they were holding up behind their back. They then add the number of fingers together and if the sum is an odd number, the person who chose odd wins and vice versa.
The surprise is, if you have never played Odds and Evens, that unlike tossing a coin in the air it is not a fair game. It is not as likely that one option or the other will come out. The probability shows that the result will more likely be even than odd.
You can see it in this table, where the numbers are marked in orange. If you look, there are 25 possible results and 13 of them are even.
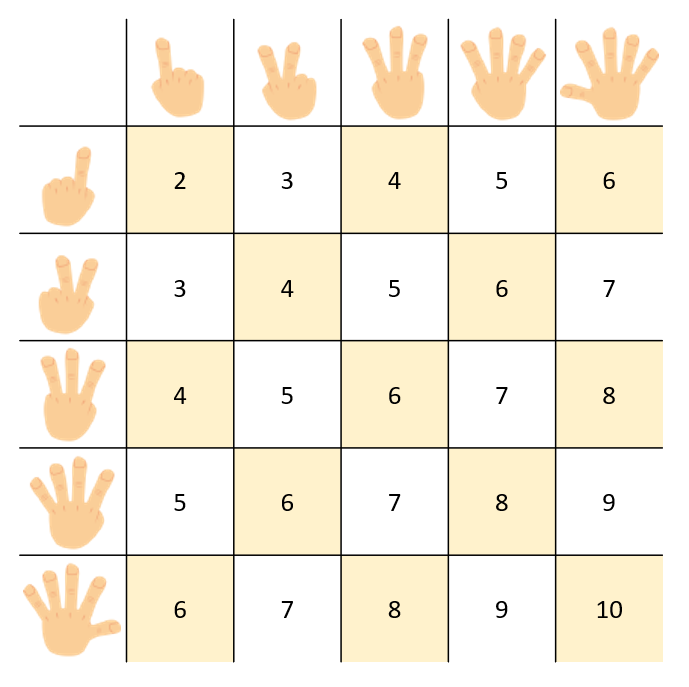
The difference is small, but if you play ‘evens’ you have 4% higher probability of winning since \(\frac{13}{25}=0,52\), while \(\frac{12}{25}=0,48\).
Example: Lottery
If you think that 4% is very small, then you shouldn’t play the lottery because the chances of you picking the right number and winning the jackpot are, \(\frac{1}{100 000}=0,00001\), a minuscule 0.001%. This number is approximately the same as picking the same drop of water from a five-liter drum.
https://www.youtube.com/watch?v=dm8ZgCLKMw0
But not all events depend on probability, many are conditions of other factors.
For example, let’s say that you want to increase your chances of passing a math test. To do this it is better to not take any chances and a great trick to getting a better grade on your math test is to do your daily math sessions with Smartick! Other ways to prepare are studying, participating in class, staying healthy, and sleeping well. If you follow these steps it is like you already know the results of tossing a coin or rolling the dice, because you know beforehand that it will work out in your favor.
Learn More:
- Learn Probability Problems and Examples
- Types of Fractions: Proper, Improper, Fractions Equal to One
- Half, Third, Fourth, Fifth in Math: Definition & Calculation
- How to Simplify Fractions with Examples
- Subtracting Fractions Exercises with Common and Uncommon Denominators
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.
- The Language of Functions and Graphs - 07/01/2024
- Educational Technology: The Christodoulou Test - 05/06/2024
- Multiplication Activities in Smartick - 04/09/2024