Today you will learn about geometric shapes. We are going to teach you about the characteristics of the main geometric shapes, and to help you understand better, we will explain with examples.
Index
What Are Geometric Shapes?
The ancient Greeks defined straight and curved lines by looking at their environment. Do you think they stopped there? Of course not! This is because straight lines are the basis for finding some figures we often find in the real world: geometric shapes.
Geometric shapes refer to planar surfaces limited by lines that can be curved or straight. To help you understand better, we are going to explain with an example.
We will start with something simple: two straight lines.
Can you create a figure with two straight lines?
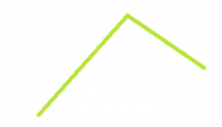
Well, of course you can! This being said, we do not call this figure a geometric shape. For this to occur, it must be closed. This is to say, that if we put a ball inside the figure, it cannot escape. In the figure we have made, a ball could escape!
If you try to move the two straight lines, you will see that there is no way to close it.
3-sided Geometric Shapes: Triangles
Now, we’re going to try three straight lines.
That’s it! Now we can create a figure that does not allow the ball to escape.
Each of the lines that we have used that now form part of the shape are called the sides of the figure. This figure has three sides and we call it a triangle. When we say “triangle,” we can refer to either the shape of the three lines or to the space they enclose.
Can you think of places where we can find triangles around us? I have found some in Smartick! Let’s see if you recognize them.
Triangle Classification
There are different ways to classify triangles according to their sides and angles.
According to Their Angles
- Right triangle: has a right angle, in other words, it measures 90º.
- Acute triangle: has three acute angles and measures less than 90º.
- Obtuse triangle: has an obtuse angle and measures more than 90º.
According to Their Sides
- Equilateral: has 3 equal sides.
- Isosceles: has 2 sides that are equal and another that is not.
- Scalene: all of the sides have a different length.
4-sided Geometric Shapes: Quadrilaterals
Now let’s try four straight lines.
For example, we could place them like this:
We call these figures quadrilaterals. There are some very special quadrilaterals that have parallel sides two by two; in other words, two sides that are parallel to each other and then two others that are also parallel. Additionally, the sides that are parallel are also equal. How could we make this shape? We take two sides and place them so that they are parallel:
How can we place the other two sides so that they are also parallel? That’s it!
When the lines are parallel and regular we have three possibilities.
Rhombus
If the four sides are equal we have a rhombus.
Rectangle
If the four angles on the figure are right angles then they form a rectangle.
Square
When both of the previous points are true, then we have a square that has equal sides and four right angles.
Video to Learn about the Classification of Quadrilaterals
Quadrilaterals are geometric figures with square sides. These polygons are classified into parallelograms and non-parallelograms. For a better understanding, I invite you to watch the following video by Smartick, the math learning method for children from 4 to 14 years old.
Regular Geometric Shapes with More Than 4 Sides
We can continue to add all the equal lines that we want to create different geometric shapes with different sides.
Pentagon
Has 5 equal sides.
Hexagon
Has 6 equal sides.
We can find them in honeycombs!
How do bees know how to create such perfect geometric shapes?
Review of Geometric Shapes with Real-Life Examples
Without us even realizing it, geometric shapes are part of our lives more than we think. Look carefully at the next image and see how many geometric figures you can find.
We are going to review a few of them.
Circle
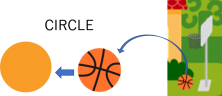
The circle is a geometric figure that is made by tracing a curve that is always at the same distance from a point that we call the center. The line that borders the circle is called the circumference.
We obtain a circle when we make a curve that maintains its distance from a specific point. For example, with a compass we choose a point with the needle and then, keeping it open, we trace the circle with the pencil. You can find circles all around you, on the wheels of your car or a tennis ball, for example.
Triangle
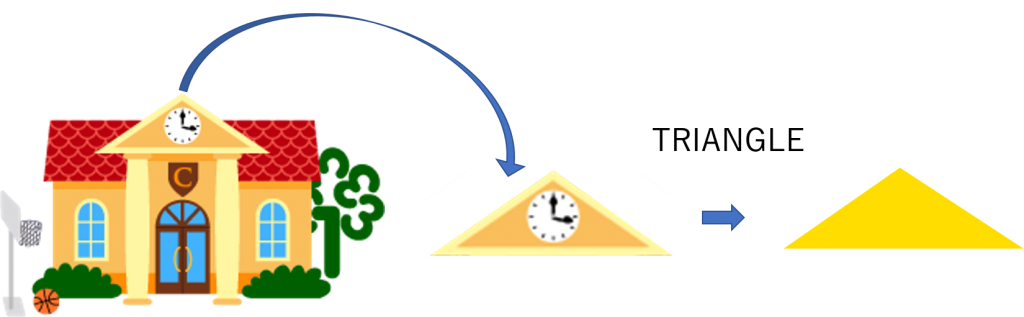
The triangle is the polygon that results from joining 3 points with straight lines. The intersection points are the vertices and the segments are the sides.
In this case, at Smartick’s school we have found an isosceles triangle. Isosceles triangles have two sides of equal lengths and one with a different length.
Square
The square is a four-sided polygon, all its sides are equal and its four angles are 90 degrees each.
Rectangle
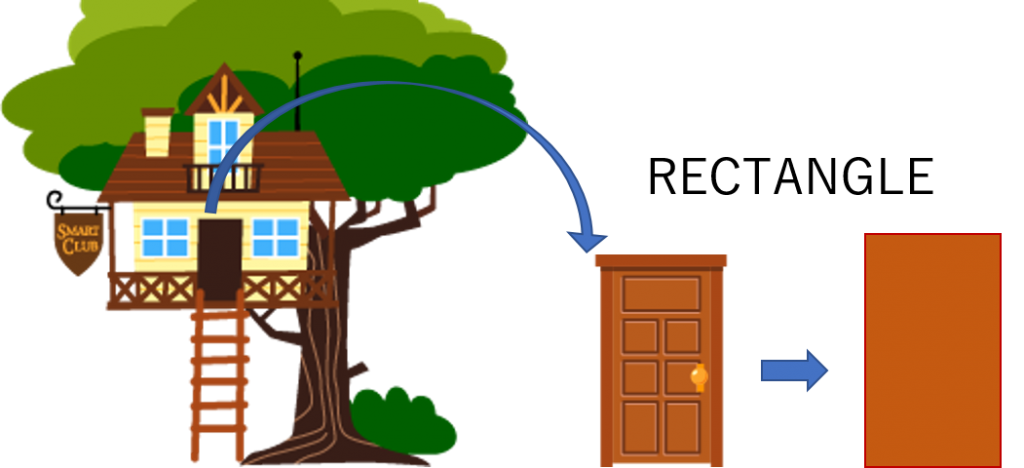
The rectangle is a figure formed by 4 straight lines called sides. The characteristics of rectangles are that their opposite sides are parallel and their 4 angles measure 90º.
Trapezoid
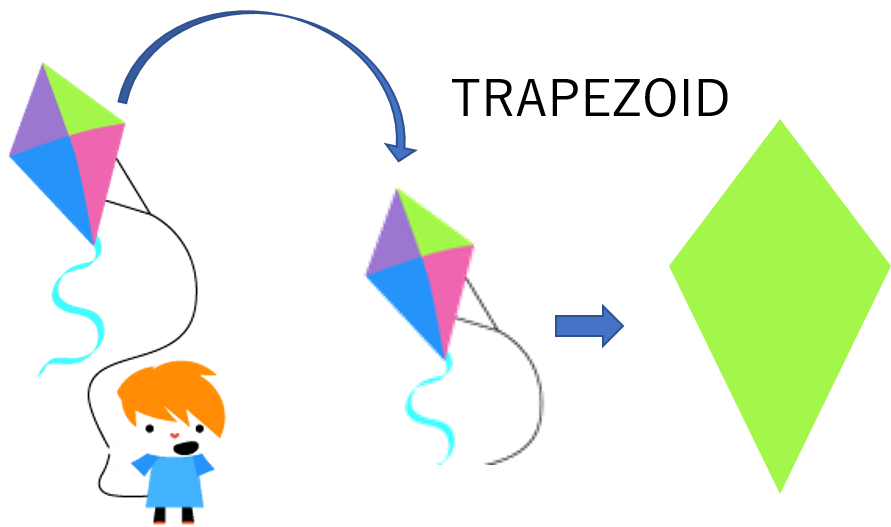
The trapezoid is a four-sided polygon, which has none of its sides parallel to another. Trapezoids can be symmetric or asymmetric, depending on their characteristics.
In this case, the kite is a symmetric trapezoid. These are trapezoids that have two pairs of equal sides and one of these pairs of sides is smaller than the other.
Octagon
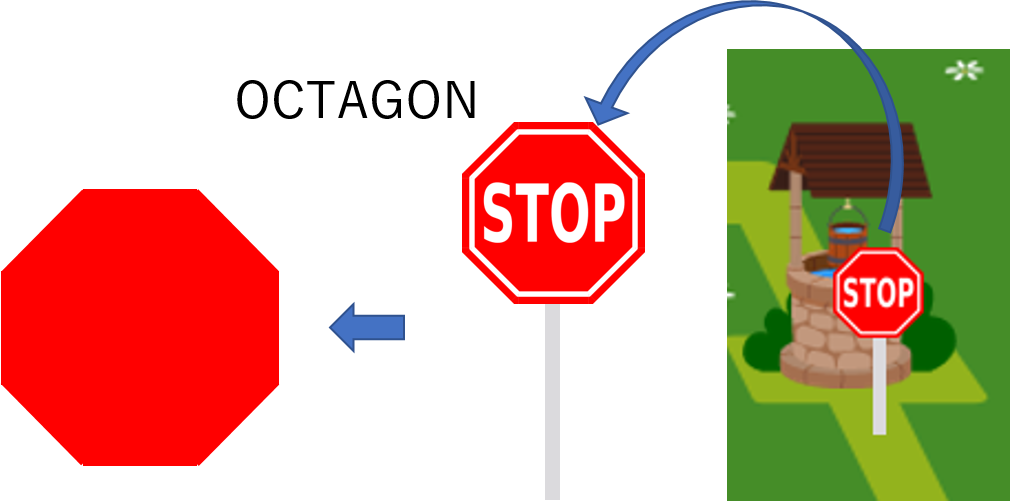
The octagon is an eight-sided polygon. The regular octagon is a polygon that has eight equal sides and eight equal angles. The sum of the interior angles of an octagon is always equal to 1080º.
We’ve found a lot of geometric shapes!!! We are sure you will find many more in your environment.
If you want, you can continue learning more elementary school math, adapted to your level, by joining Smartick!
Learn More:
- Geometric Figures and Straight Lines
- Geometric Plane Shapes: Circles, Triangles, Rectangles, Squares, and Trapezoids
- Discover Geometric Figures Found in Our Environment
- Geometry and 2D Shapes with the Help of a Tangram
- Geometric Shape: Properties of a Square
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.