In this post, we are going to learn about straight and curved lines which Euclid described and studied.
Many, many years ago (more than 2,000 years) there was a culture to which we owe an important part of mathematics, Ancient Greece. It is likely that Euclid’s contribution was the most important. He collected everything that was known about mathematics up until that point and compiled a collection of books called The Elements.
Euclid dedicated many of his books to geometry (the Greeks loved it!). His work on this discipline remained intact until the 19th Century, and what was done afterward belongs to advanced mathematics and is studied at university. This means that pretty much everything we study in geometry at school now was written over 2,000 years ago! This is why flat and spatial geometry is often called Euclidean Geometry.
Index
What are Lines?
Every line is composed of points, which is the smallest unit. One point, Euclid said, has no dimension: no height, width, or depth. So those points can only live in the imagination of mathematics because they are infinitely small.
A line consists of a succession of points. These points are so close together that when you see them they form one continuous stroke. Even when using a magnifying glass you still would not be able to see the space between the points they are so close together.
Video about Types of Lines and Their Classification
To learn more about what lines are and how to classify them take a look at the following video. This is a video of one of our interactive tutorials. Although it is not interactive this way, you can still watch it as many times as you need to and share it with friends. If you would like to access our interactive tutorials, register with Smartick! The online method that helps children ages 4 to 14 learn and practice mathematics.
Types of Lines According to Shape
Straight Line
A straight line is a succession of infinite points that are all plotted going in the same direction. They do not have a beginning or end, in other words, they have no limits.
Straight lines are endless so you can never draw a complete straight line, only a portion of it and we need to imagine the rest.
Curved Line
A curved line is a succession of infinite points that continuously change direction.
In the definitions we talk about the directions of alignment that the point should follow but what exactly does that mean?
The following image will help us understand it better.
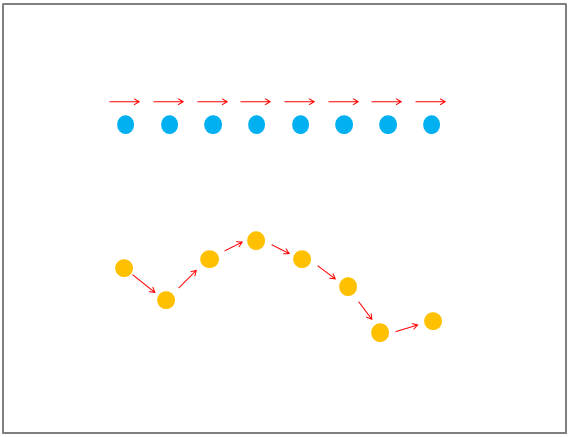
If we look at the arrows above the blue points (straight line) we can see that a point maintains the same direction as the previous without varying. The arrows do not change direction.
However, the direction of the arrow with the orange dots (curved line) does not remain constant. And this is the difference between straight and curved lines.
But this isn’t the only way to do it! The original way (the one used today in mathematics) is much similar to that used by Euclid. Think of two points on a piece of paper, how many ways can you get from one to another?
If there aren’t any obstacles we could use many different ways. For example:
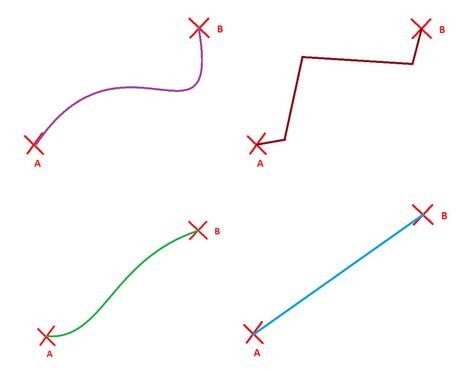
And many more, right? Now the key question of all the lines that we have drawn which is the shortest? In other words, what is the shortest distance between A and B? That’s it! The last line, the blue one. Here is another way to define a straight line, which is the shortest path between two points:
Between two points, the line is straight if it is the shortest path between them.
If it is not the shortest path then it is not a straight line.
Wait! What about the second line we’ve drawn? This is a special case because it is not one, but multiple lines.
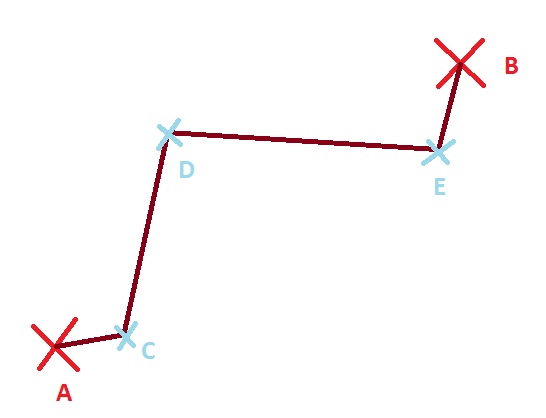
- The line that joins A with C.
- The line that joins C with D.
- The line that joins D with E.
- The line that joins E with B.
This case is called a polygonal line.
If you would like to learn more, check out our posts about straight lines and curved lines.
Remember when we said before that Euclid Geometry was flat geometry? If points A and B used to be on the surface of a sphere – for example, a ball – you wouldn’t be able to draw a straight line without going through the ball!
Types of Straight Lines in Space Depending on the Arrangement
Horizontal Line
Horizontal lines are those that are drawn in the direction of the horizon, left to right, or vice versa. They are perpendicular (a 90-degree angle) to vertical lines.
Vertical Line
Vertical lines are those that are drawn up down or down up.
Oblique Line
Oblique lines are those that do not have a vertical or horizontal direction and do not or right angles when they intersect.
All straight lines divide the plane into two parts. To understand this, if you draw a straight line on a piece of paper – and you don’t do it near one of the edges – you will divide the paper in two. If it is a horizontal line, you have a part above and below, and if it is vertical, you have parts on the left and right.
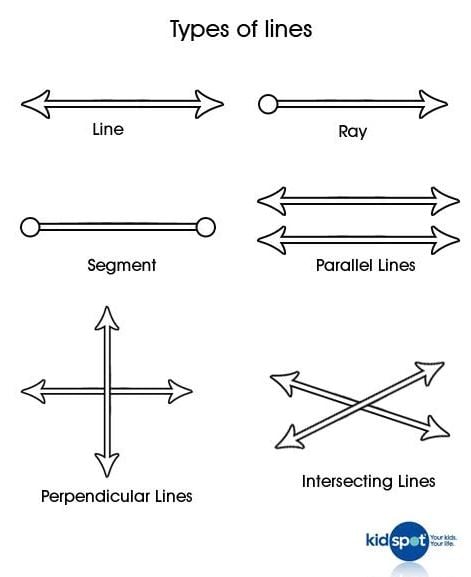
Types of Straight Lines According to the Position Between Them
Parallel Straight Lines
Parallel lines are on the same plane and maintain a certain distance between them because they never intersect or touch at any point. Not even their extensions.
An example of parallel lines would be train tracks even if they appear to touch in the distance. Have you ever heard that straight lines touch infinity? It is because of the feeling that train tracks get closer but it isn’t true. Besides infinity is not a point, so saying that they touch infinity is a strange way of saying that they do not touch.
Straight Secant Lines
The secant lines are cut at one point and the two lines form four angles none of which are right angles.
Perpendicular Straight Lines
Perpendicular lines are a particular case of secant lines, in addition to being cut at one point they form four right angles (90-degree angle).
In all of these drawings, we have segments, pieces of lines that end. If we tried to draw complete lines we would never finish because they are infinite.
Video About the Relationships Between Lines
To keep learning take a look at this video where Amy and Zoe learn about the relationship between lines.
If you would like to see more of our interactive tutorials and continue learning about geometry and other math topics adapted to your level, register with Smartick and try it for free.
Learn More:
- Elementary Geometry – Open Lines
- Learn More about Straight Lines
- Learn about Open and Closed Curves
- Symmetry: What It Is And How to Find It
- Geometric Figures and Straight Lines
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.
Thanks for reminding us of the basic mathematical history in a simplified manner.
That was comprehensive. Need more
Hi Utthaan:
If you want to learn more about geometry and much more you can do so by trying our free trial in https://www.smartick.com
Thank you!