In today’s post we are going to talk about the foundations of the Singapore Method.
First off, here is a bit of history: Singapore is a very small country situated between Malaysia and Indonesia that lacked (and still lacks) natural resources. In 1965 Singapore was an island of fishermen, and now it has one of the busiest ports in the world, besides being one of the most prosperous city-states in Asia.
How did Singapore achieve this?
Among other things, Singapore decided to bet on education; the nation undertook an educational reform, and education became one of the country’s fundamental pillars. Now Singaporeans systematically lead in the International Standard Classification of Education.
“Schools that think, nation that learns”
These are the foundations of the Singapore Method—of the methodological focus applied to math instruction in Singapore:
Learning in Three Stages (Jerome Bruner)
Different concepts are introduced through the CPA Approach.
During the first stage, students must use concrete materials, manipulatives, and objects from everyday life.
In the second stage, students make pictorial representations, such as drawings or images that help them solve a problem.
In the third stage, students get to the abstract understanding of the concept that has been worked on.

Developing the Understanding of a Concept and the Learning of Procedures in Parallel (Richard Skemp)
Instrumental understanding (know-how) is the ability to perform an operation (such as long division or dividing fractions).
Relational understanding (know-what) is the ability to explain the procedure.
Relative math is easier to remember, even though it is more difficult to learn. However, instrumental math allows us to provide the correct answer in a way that is faster than we would through relational thinking.
In the Singapore Method (and at Smartick), these two types of understanding always go hand in hand.
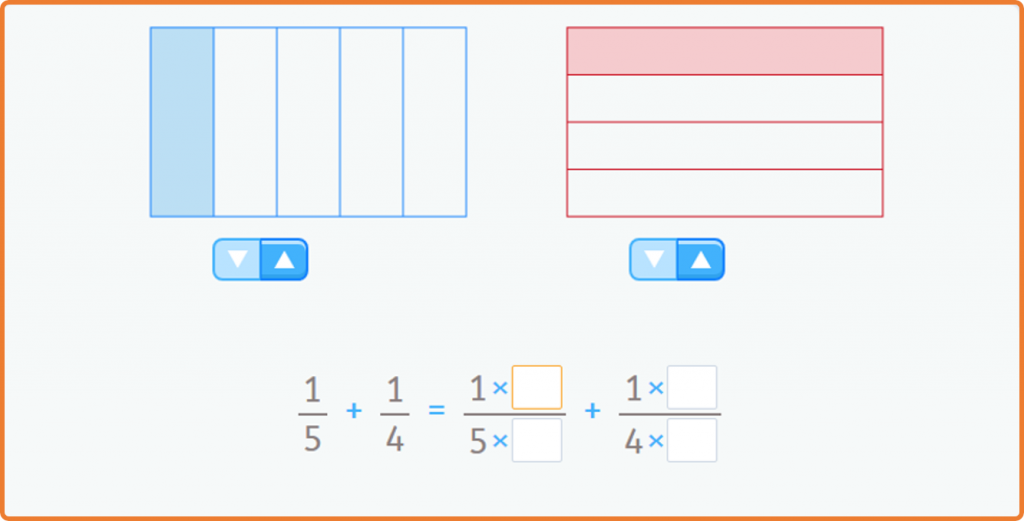
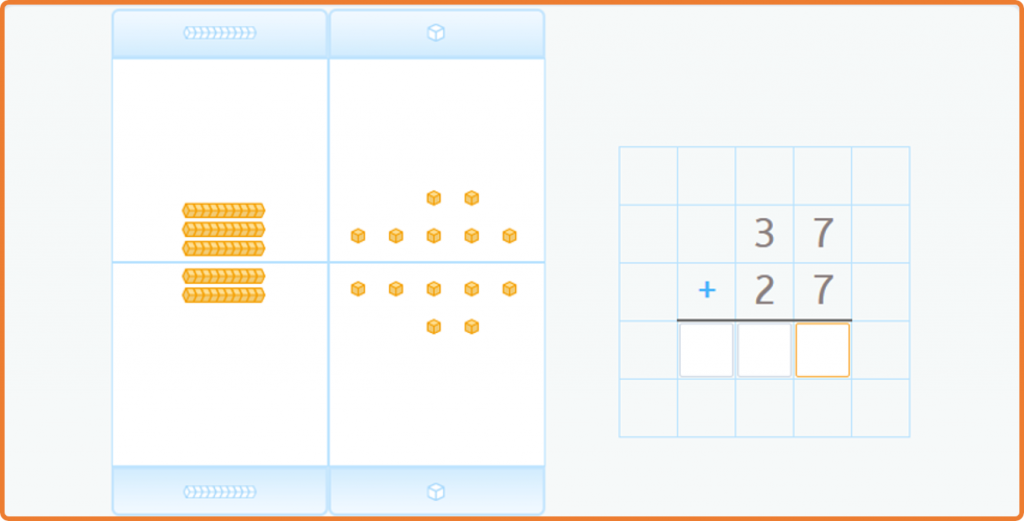
Variety of Presentations (Zoltan Dienes)
The understanding of a concept will be better if it is presented from different points of view. For example, to solve an addition problem we can draw marks and count all of them. Another option would be to solve the problem with our fingers, by putting 4 up on one hand and 2 up on another, and counting them altogether.
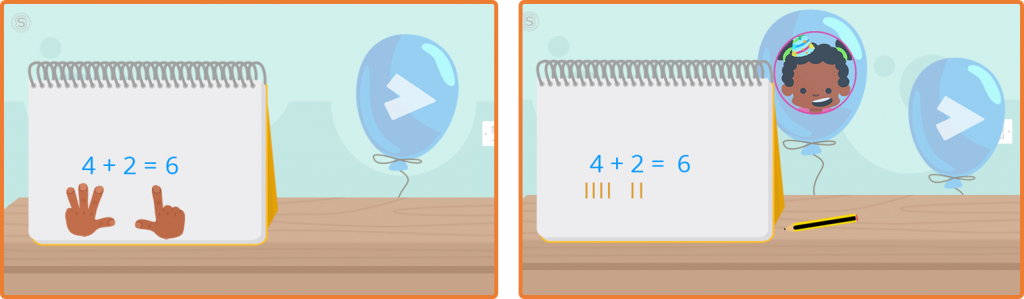
Zone of Proximal Development and Scaffolding (Lev Vygotsky)
Students build their learning through interactions that help them progress from the current area of development (which represents what the student knows) to the potential area of development (which represents what the student could come to know).
Now, let me show you an example of a Smartick didactic sequence.
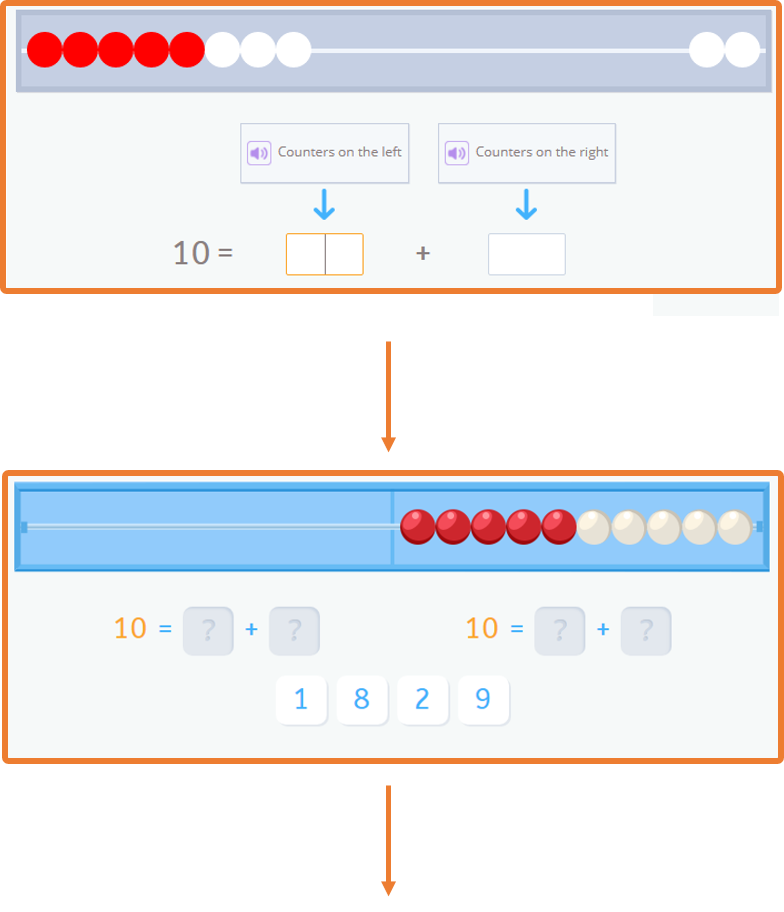
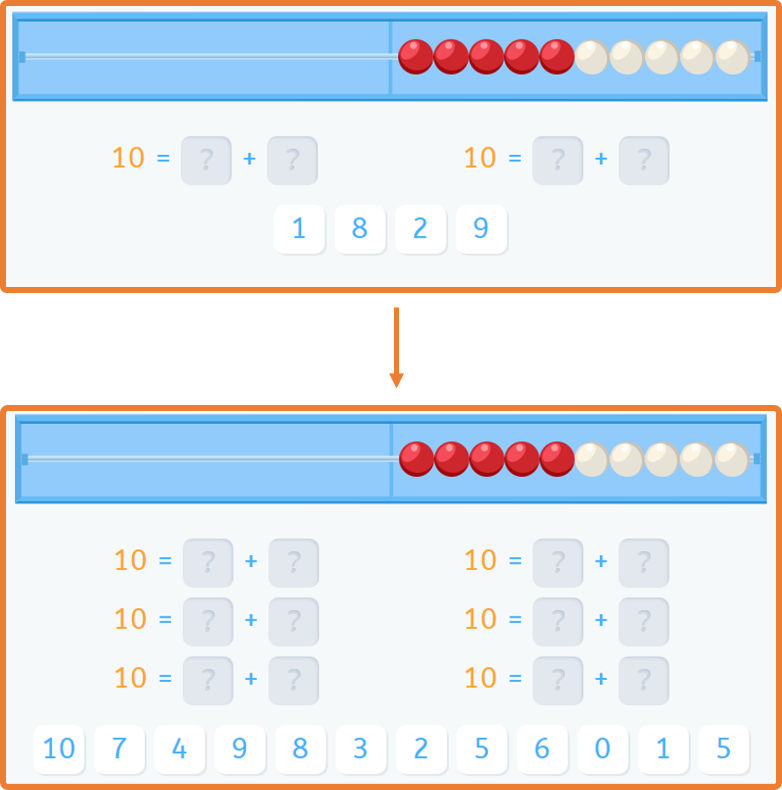
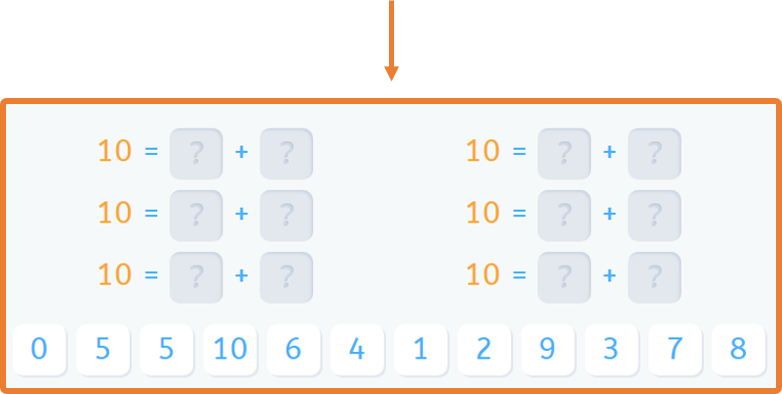
Did you like this blog post about the explanation of the Singapore Method? If you would like to continue learning math, go to Smartick and try it for free.
Learn More:
- Singapore: Math Curriculum in Primary Education
- Singapore Method: Using the Singapore Bar Models to Solve Problems
- Teaching Principles and Learning Phases of Singapore Math
- Using Singapore Bars to Solve Algebraic Equations
- Theoretical Framework of the Singapore Method








That’s the best answer of all time!