In previous posts, we’ve talked about how to use the Singapore Method with different math operations. In today’s post, we’re going to look at what kinds of advantages this method boasts for solving problems.
We know that problem solving is one of the most important parts of math. So, we need to provide students with tools that help them learn and understand math concepts. A way to improve student’s problem-solving abilities is by helping them visually represent the problems.
The Singapore Method is used to represent and solve problems that have complicated structures by drawing out a pictorial model that allows students to process information. It helps students make some sense from the known and unknown quantities and relate them.
This method helps students get a better understanding of math concepts, plan their problem-solving steps and it clears up the algebraic method. All of this can lead to great leaps in motivation when students face challenging problems.
Let’s take a look at some examples using the Singapore Bar Models to solve the problems.
Maria’s going to celebrate her birthday at home and invited 20 classmates. If we know that 3/5 of the class are girls and the rest are boys, how many girls did Maria invite to her party?
The first thing that we need to do is draw a bar that represents all of the classmates that Maria invited to her party:
- After drawing the bar, we divide it into 5 parts because the problem tells us that 3/5 of the guests are girls:
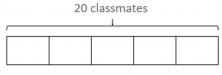
- And now, we color the part of the bar that represents the number of girls, 3/5.
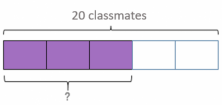
- Once we have the problem set up graphically, we can determine the best way to solve it. Alright, we know that the total number of guests is 20 classmates, which we represented with the first bar, and we divided it into 5 parts. Now, we can describe how many classmates represent one part of this whole:
5 parts = 20 classmates
1 part = 20 ÷ 5 = 4 classmates for each part
3 parts = 4 x 3 = Maria invited 12 girls to her birthday party
The rest of the guests are boys= A total of 20 guests – 12 girls= Maria invited 8 boys to her birthday party
Another example using the Singapore Method:
William has 130 model cars in total. He has 4 times as many convertibles than cars that aren’t convertibles. How many convertibles does William have?
We need to draw a bar for the convertible cars and divide it into 4 parts because the problem tells us that William has 4 times as many convertible cars tan cars that aren’t convertibles:
- Now that we’ve represented the number of convertible cars that William has, we can represent the number of cars that aren’t convertibles. We need to remember that he has 4 times as many convertibles than cars that aren’t convertibles, so we need to draw a bar that represents one part of all the convertible cars:
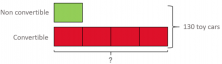
- Now we have all our representations set, we can solve the problem:
The total of all the parts is 130 cars, that’s to say that 5 parts = 130 cars.
1 part = 130 ÷ 5 = 26 cars
4 parts = 26 x 4 = 104 convertible cars
That’s all for examples of problem-solving with the Singapore Method. We’ll check out some more another day.
If you want to keep learning math, make an account at Smartick to try a free trial!
Learn More:
- Using Singapore Bars to Solve Algebraic Equations
- Using Singapore Bars to Help Solve Problems II
- Singapore Bars Applied to Fractions
- Singapore Bar Model and Percentages
- Word Problems with Fractions
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.
- The Language of Functions and Graphs - 07/01/2024
- Educational Technology: The Christodoulou Test - 05/06/2024
- Multiplication Activities in Smartick - 04/09/2024