In this post, we will look at what monomials are, what their components are and what properties they have.
Index
What is a Monomial?
A monomial is a combination of numbers and letters related by only multiplication and the exponents of the letters can only be natural numbers.
For example:
-5ax 3
Is a monomial because it is a combination of numbers and letters related to each other only by multiplication and the exponent that appears is a natural number.
-2m 5 + m 3
It is not a monomial because both addition and subtraction appear.
In the following exercise, decide if the algebraic expressions are monomials or not:
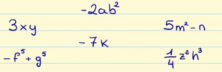
Parts of a Monomial
Coefficient
The number the letters are multiplied by.
Literal Part
The letters are displayed in the monomial with exponents.
Degree
The sum of the exponents that the monomial has.
Variable
Each of the letters in the monomial.
Example of a Monomial
Let’s look at the parts of the following monomial:
-2ab 2
- Coefficient: -2 is the number that accompanies the literal part.
- Literal part: ab 2
- Degree: 1 + 2 = 3. The degree of the monomial is 3.
- Variable: a, b. They are the two letters that appear in the monomial.
What are two similar monomials?
Two monomials are similar when they have exactly the same literal part.
For example, a similar monomial for one that we’ve seen before, -2ab 2, would be any which had the same literal part: ab 2
Like the monomials: -6ab 2 , 5AB 2 , 18ab 2 , ab 2 …
Now, I propose that you connect the monomials in the left column with their similar monomials in the right column.
And with that, we have finished this post. If you liked this post, share it with your friends and family! And if you want to learn more math, try Smartick for free.
Learn More:
- Review the Properties of Polynomials
- Learn How to Add Polynomials with Examples
- Representing Polynomials with Algebra Tiles
- Algebraic Expressions: What Are They? What Are They Used For?
- Reducible Equations: What Are They? How Do We Solve Them?
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.