Mathematics is a universal language that allows us to describe and understand the world around us. One of the fundamental branches of mathematics is algebra, and a key tool in this discipline is algebraic expressions. In this article, we will explore what algebraic expressions are, what they are used for and how they are used in the real world.
Algebraic expressions appear in the transition from primary to secondary school or in middle school, around the age of 12. And once they appear, they are here to stay. As with most things that are new and different, algebraic expressions raise a lot of questions and are feared by students, so it is best that we start by clarifying what they are and what they are used for.
Index
What Are Algebraic Expressions?
Algebraic expressions are combinations of numbers, variables and mathematical operations, such as addition, subtraction, multiplication and division. They are represented by symbols and letters, where numbers are considered constants and letters represent variables, that is, values that can vary. They follow all the arithmetic rules we have learned so far, however now some numbers are replaced by letters that can be of different values. It will be better explained with examples:
- Addition of two numbers: if we have two numbers, for example, 3 and 5, we know that to add them we must write 3+5. We know that their sum is 8. If the two values are not known, we can also add them, although now we do not know the result. We can represent these two numbers with the letters x and y, which, and since they do not have a fixed value, will be called variables. If we want to express the sum of these two numbers, we can use the algebraic expression: x + y. Notice that we use two different variables because we have not been told that they are the same number, only that we want to get an expression for the sum of “two numbers”.
- The double of a number: 2x
- Area of a rectangle: In the same way that we would calculate the area of a rectangle with a base of 4 and a height of 2 we would multiply 4 by 2, if we want to calculate the area of a rectangle with base “b” and height “a”, we can use the algebraic expression: A = b x a where “A” represents the area of the rectangle.
- Formula for the area of a circle: If we know the radius of a circle, represented by “r”, we can use the algebraic expression: A = π – r2 to calculate its area. Here, “A” denotes the area of the circle and π is a constant representing the approximate value of pi, we usually take 3.1416.
- Temperature conversion: Let’s say we want to convert the temperature from degrees Celsius to degrees Fahrenheit. We can use the algebraic expression: F = (9/5) – C + 32, where “C” represents the temperature in degrees Celsius and “F” represents the equivalent temperature in degrees Fahrenheit.
What Are Algebraic Expressions Used For?
As you may have already guessed from the examples, algebraic expressions are used to describe mathematical situations and relationships in general terms. That is, in situations where not all values are known. They allow us to express formulas, equations and mathematical models in an abstract way, which facilitates analysis and problem-solving.
An example of the usefulness of algebraic expressions would be, for example, to obtain new formulas. Since we know that the volume of prisms and cylinders is the area of the base (Ab) times the height (h) V = Ab- h, we can substitute in that formula the area of the base. If we know that the base is a circle, Ab= π – r2, we can substitute and write in a single formula that the volume of the cylinder is V = π – r2 – h.
Components of Algebraic Expressions
- Constants: These are fixed numbers that do not change their value, such as 2, 5 or π.
- Variables: These are letters that represent unknown quantities or variables, such as x, y, and z. These variables allow us to generalize and solve problems for different values.
- Mathematical operations: These include addition, subtraction, multiplication, division, and exponents, among others. These operations are applied to constants and variables to form more complex expressions.
What is not included in algebraic expressions is equality, the examples we looked at before that contained the equal sign what they had on the left is interpreted as the result of that expression, when we have on the left another expression, we will be talking about equations, and we will deal with it at the end of the article.
Simplification of Algebraic Expressions
Algebraic expressions can be simplified by using distributive, associative and commutative algebraic properties and rules. Simplification helps to reduce the expression to a more manageable and understandable form. In algebra, the arithmetic rules are followed. Therefore, if it is valid for numbers, it is valid for algebraic expressions, x + x is 2x.
Real-World Applications
Algebraic expressions have numerous real-world applications. Some examples include:
- Physics: In describing physical laws and phenomena, such as the law of universal gravitation or the equations of motion.
- Economics: In modeling financial problems, such as calculating interest, profits or depreciation.
- Engineering: In the design and analysis of structures, electrical circuits or control systems.
- Computer Science: In algorithms and programming, where algebraic expressions are used to perform calculations and make decisions.
A Particular Case, Monomials
Monomials are a particular case of algebraic expressions that only use the product, and in which the exponents of the variables that appear have to be natural numbers (therefore positive). Of the algebraic expressions seen here, there would be monomials, all except this: (9/5) – C + 32, additionally x + y because it contains a sum – Neither would be 1/x because written as a power it is x-1, which is not a natural number. You can see more information about monomials in this blog post.
Algebraic Expressions and Equations
Now we will look at an application that it deserves its own section, equations. Equations are not algebraic expressions, because they are instead two (or more) algebraic expressions joined by the equal sign. It will be better understood, just like everything else, with an example:
We said above that the double of a number is 2x. How would we say “one number is the double of another”? It cannot be x = 2x, because that would be a number is equal to its double. But we can say y = 2x, because by using two different variables (letters) we are denoting exactly that. If, for example we consider the pairs of points (x,y) that fulfill that equation, that equality between algebraic expressions, we would have the (1,2), the (10,20), the (π, 2π) and ALL the pairs in which the second coordinate is two times the first. We can even paint it, taking, as it is usually taken, the first coordinate on the x-axis and the second on the y-axis:
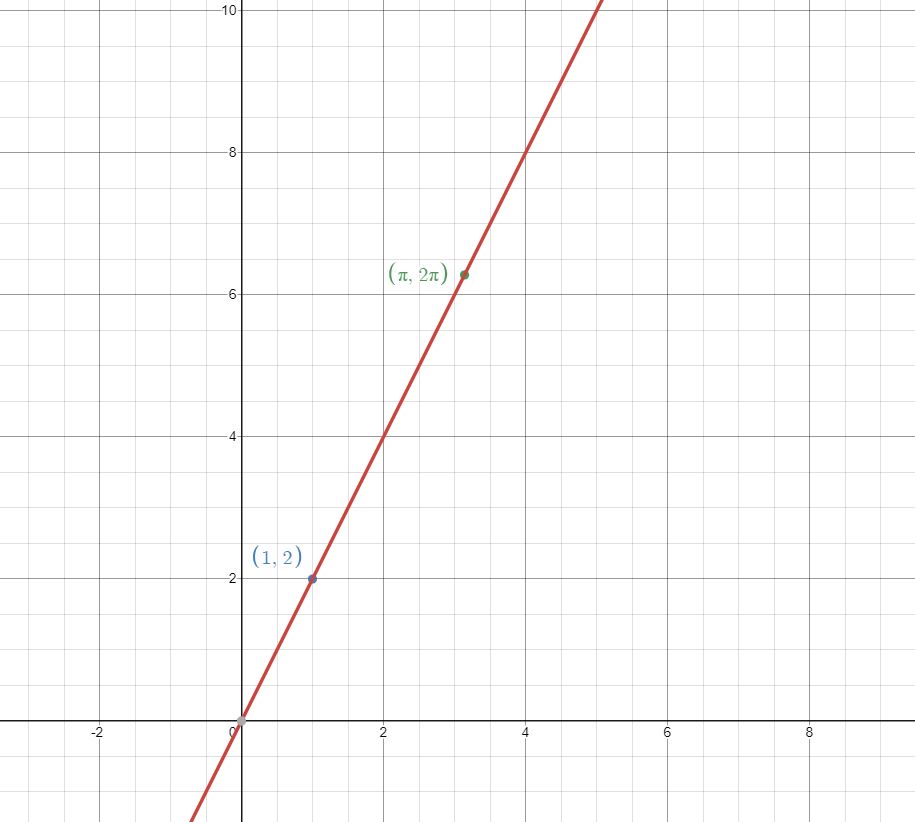
Stretching the idea “a little” we could try to envision the following equation, which is still an equality between algebraic expressions, although it is much more difficult to translate with words:
You can try changing some of the values of the expression in the desmos graphing calculator.
I hope you have found the post interesting, feel free to share it or leave a comment your doubts or questions, or the topics you would like to know more about. Tofind out more, sign up for Smartick, the online math learning method for children from 4 to 14 years old.
Learn More:
- Algebra Problems: 3 Types of Activities in Smartick
- Introduction to Equations with an Example
- Review the Properties of Polynomials
- Learn the Properties of Monomials
- Learning the Temperature Scales: Degrees Celsius or Fahrenheit?
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.