In the U.S. the most common units for measuring mass are the ounce (oz) and the pound (lb). Technically, the pound is a measure of force, not mass, and the ounce can be a unit of volume or weight, which makes things even more confusing! But I won’t nitpick here! What is more important is that elsewhere in the world—that is almost everywhere in the world—the metric system is used, even in England! It is part of the United Kingdom, which is where the pound and the ounce came from (along with feet and inches)!
In the metric system, the main unit used to measure mass is the gram (g), but it’s not the only one! There are multiples and sub-multiples, among which are the kilogram (kg) and the milligram (mg).
Are they all the same? Is 1 kilogram the same as 1 gram or 1 pound?
Of course not! But there are conversions between each one:
1 kg = 1000 g 1 kg = 2.2 lb
1 g = 1000 mg 1 ton = 2000 lb
Conversions allow us to solve problems that have different mass units.
Therefore, when we have to solve problems related to mass measurements, it is very important that we look at what unit or units the mass is expressed in and, using the conversions, move from one to the other when necessary.
For example, if we buy the following in the supermarket and we ask, “Which has more mass? The pineapple or the bag of flour?”
This is very easy because the mass of both products is expressed with the same unit, in this case, kg.
Since we know that 3 > 1 the correct answer is the pineapple.
But what if what we buy is this:
Which has more mass?
To find out, what we would have to do is convert the kilograms to grams or vice versa, to compare.
We convert the kilograms to grams:
1 kg = 1000 g therefore 2.2 kg = 2200 g
Now we can compare and 2200 > 1750, so the correct answer is the cheese.
Sometimes the mass is expressed by combining kilograms and grams.
For example:
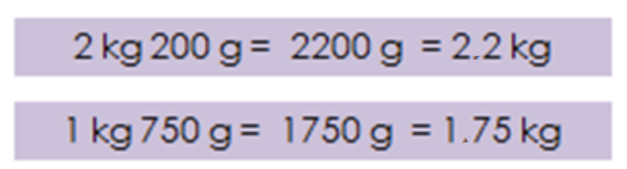
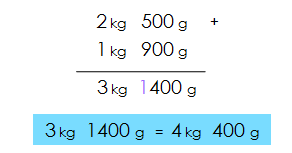
If we want to know the mass of the cheese and cake together, we could convert it all to grams or kilograms and add
2200 g + 1750 g = 3950 g
Or we can add kilograms with kilograms and grams with grams, as follows:
If the sum exceeds 999 grams, we would have to convert them to kilograms. For example:
Now imagine that we want to make an apple pie but since the recipe is in Spanish, it has the ingredients in kilograms, but you need to know how many pounds that is. It says we need 4 kilograms of apples. How many pounds of apples do we need?
We see that once again equivalences are needed to know to answer.
1 kilogram = 2.2 pounds
Multiply 4 x 2.2 = 8.8
And we know we need to buy 8.8 pounds of apples.
Knowing the equivalences between mass units can be very useful!
Since you already know some, try to solve this situation:
Frederic is taking a trip to Europe. The airline said he can only bring 1 suitcase and that suitcase cannot exceed 20 kilograms. Frederic knows his empty suitcase weighs 4 lb and has already pulled all the things he needs out of the closet. Now he has to decide what to pack and what he needs to wear since he cannot put everything in the suitcase because it would exceed the limit. Considering that he wants to dress as light as possible on the traveling day, what would he wear?
Leave your answer in the comments and together we will discover the best choice for Frederic.
Have a great week!
And if you want to practice much more mass measurement problems, try Smartick for free!
Learn More:
- How to Solve Mass Conversion Problems
- Learn How to Convert Mass Measures in the Metric System
- Conversion Capacity Problems in the Metric System
- Learn about the Metric System and Measurements of Volume and Mass
- Practicing with Units of Measurement in the Metric System
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.
- The Language of Functions and Graphs - 07/01/2024
- Educational Technology: The Christodoulou Test - 05/06/2024
- Multiplication Activities in Smartick - 04/09/2024