In today’s post, we are going to look at some examples of capacity measurement conversion problems, and offer some advice about how to solve them.
Remember, we have already seen how to solve problems converting length measurements and mass measurement conversion problems.
Before starting problems, look back at the scale of the main units of capacity measurements. You can use it to help with conversions.
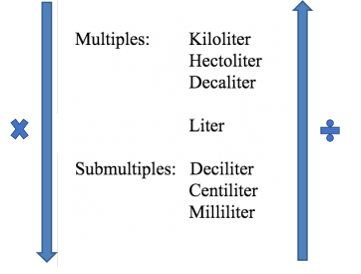
To convert in descending order (larger measurement to smaller) it is necessary to multiply and to convert in ascending order (smaller measurement to larger) you must divide.
Prepared? Well let’s look at the conversion problems that we have today:
Capacity Problem: Pots and Pans

Pete bought a complete set of pans for when he moves into his new home. The smallest pan has a capacity of 15 deciliters which is 2.8 liters capacity less than that of the largest pan in the kit. What capacity does the largest pan have? Express the result in both units.
Because we have to express the result in liters (l) and deciliters (dl), we can convert to the unit we want first. For example, let’s turn l into dl. Since we have to move up the scale, we have to divide:
10 dl = 1 l … Then 15 dl = 15/10 = 1.5 l
Now we add:
2.8 l + 1.5 l = 4.3 l
Now back to convert to dl. And since you are moving down the scale, multiply:
4.3 l = 4.3 dl = 4.3 x 10 dl = 43 dl
Therefore, the answer to this problem is:
4.3 liters, which is equal to 43 deciliters
Capacity Problem: Coffee

In the Roma Café, if you order a “Lungo” (long) Coffee, they pour you a cup of coffee with 7.5 cl, exactly 3 times as much coffee as if you ask for a “Simple Espresso”, which is much more concentrated. There is also a “Maxi-Expresso” coffee, which has 35 ml more than the “Simple Expresso”. How many milliliters of coffee are there in a “Maxi-Expresso”? Express the result in liters as well.
We begin by calculating the coffee in a “Simple Expresso”:
7.5 cl / 3 = 2.5 cl
Now, we add 35 ml to this amount, but in order to complete this operation, the quantities must be expressed in the same unit of measurement.
Therefore, we will convert 2.5 cl to ml. Since you move down the scale, we have to multiply:
1 cl = 10 ml … Then 2.5 cl = 2.5 x 10 ml = 25 ml
Now we can add:
35 ml + 25 ml = 60 ml
To convert the result to liters, we have to move up the scale, in other words, divide:
1 l = … 1000 ml… then 60 ml = 60: 1000 l = 0.06 l
Therefore, the answer to this problem is:
60 milliliters or 0.06 liters
And with that, we’ve completed this post on capacity measurement conversions.
If you want to keep learning, sign up for Smartick and try it for free!
Learn More:
- How to Solve Mass Conversion Problems
- How to Solve Problems with Distance Conversions
- Time Measurement Problems: Simple and Complex Forms
- Practice Length Measurement Problems
- Learn about the Metric System and Measurements of Volume and Mass








I want to allow him to be better in word problem