Scientific evidence tells us that children with learning difficulties who do not use mental math strategies have poor results in this area, similar to those of children with learning difficulties specific to math. That is why at Smartick we wanted to make sure that all children develop mental math strategies.
In this post, we are going to see some mental math strategies, how to prepare children to learn them, and the types that we work on in Smartick.
Index
What Are Mental Math Strategies?
Mental math strategies consist of the use of number facts to solve more complex operations.
Numerical facts are numerical relationships that we have committed to memory that vary from person to person, however, there are some that we all have in common. For example:
- “Five and five is ten.”
- “Two and two is four.”
- “Three times four is twelve.”
At Smartick we explicitly teach mental math strategies. We focus on the most popular numerical facts which are common to most people. Such as doubling numbers up to five (two and two is four), the addition of numbers less than five with five (five and three is eight), and additive decompositions of the number 10 (six and four is ten).
However, in order to acquire these numerical facts, some prerequisites are important to prepare our mathematical thinking. First, internalizing these numerical facts, and second, applying them to solve operations in order to develop mental math strategies.
What Do We Need to Learn Mental Math Strategies?
As we have mentioned, in order to learn and develop mental math strategies, we need to have certain numerical facts acquired. We work on this in Smartick focusing on learning:
Numerical Sense
Numerical sense refers to the cognitive process used to move from identifying quantities associated with numbers to establishing relationships between them. It helps to answer the question “What is seven?”
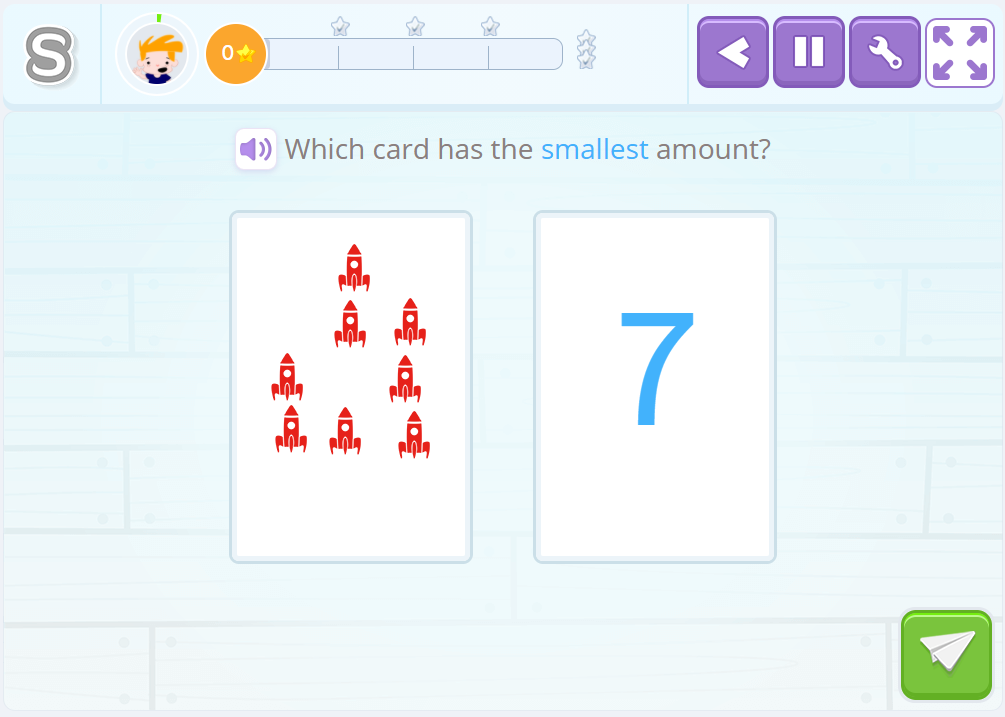
Additive Decomposition
This refers to the way in which 7 can be expressed, for example: “seven is 3 plus 4, but also can be 5 plus 2 or 6 plus 1.”
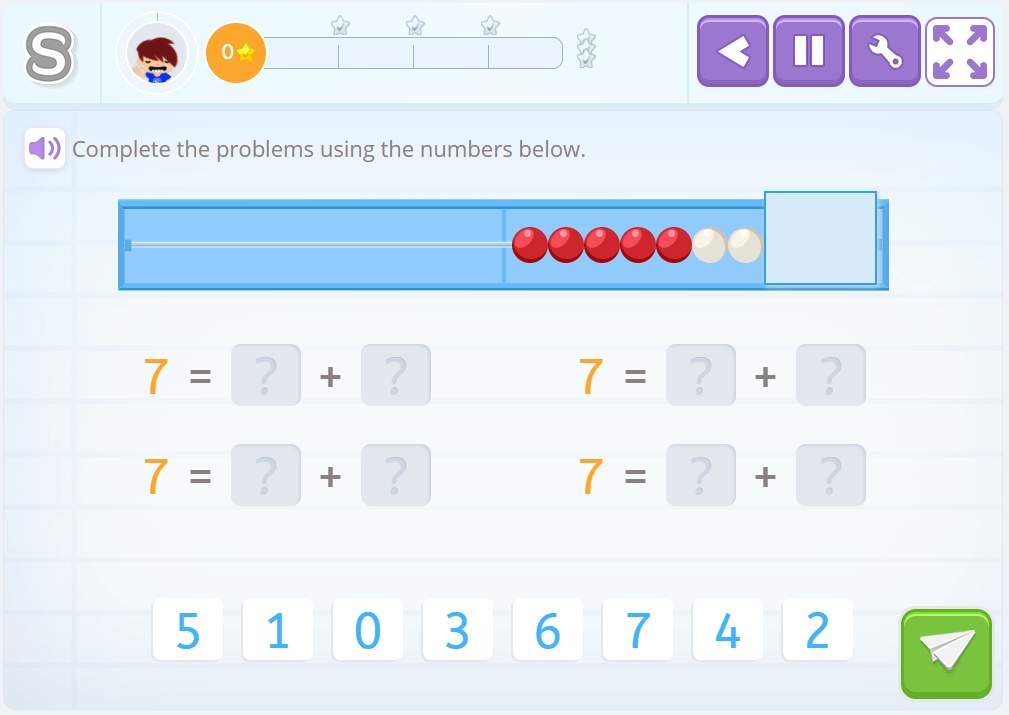
Subitization
Subitzation refers to the ability to quickly detect the amount that is being represented. In Smartick we use the rekenrek, among other materials, since it gives us a very clear reference to the quantities 5 and 10. These are very important numbers in the acquisition of numerical facts and therefore, the learning of mental math strategies.
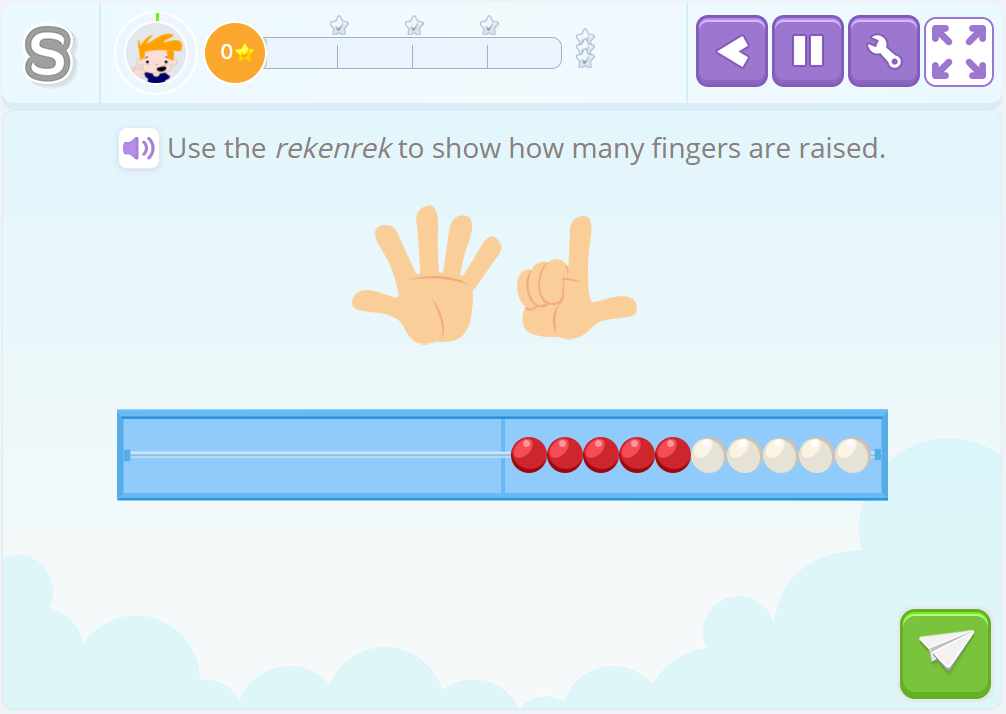
So, once a child has acquired these skills they are prepared to memorize the basic numerical facts and use them to solve other operations.
What Type of Mental Math Strategies are Developed in Smartick?
In Smartick we are developing additive mental math strategies and to make it more manageable, we have divided them into six blocks: three blocks for addition and three for subtraction. These blocks have been established based on the value of the numbers used and among them are the different types of strategies that can be distinguished by how the numbers are treated.
The two main strategies we find in Smartick are decomposition strategies and jump strategies. Compensation strategies for mental math also exist but they are not practiced with the same intensity in Smartick.
Decomposition Strategies
Decomposition strategies have this name because the factors in the operation (addends, minuends, and subtrahends) decompose additively in search of numerical facts. Let’s look at some examples.
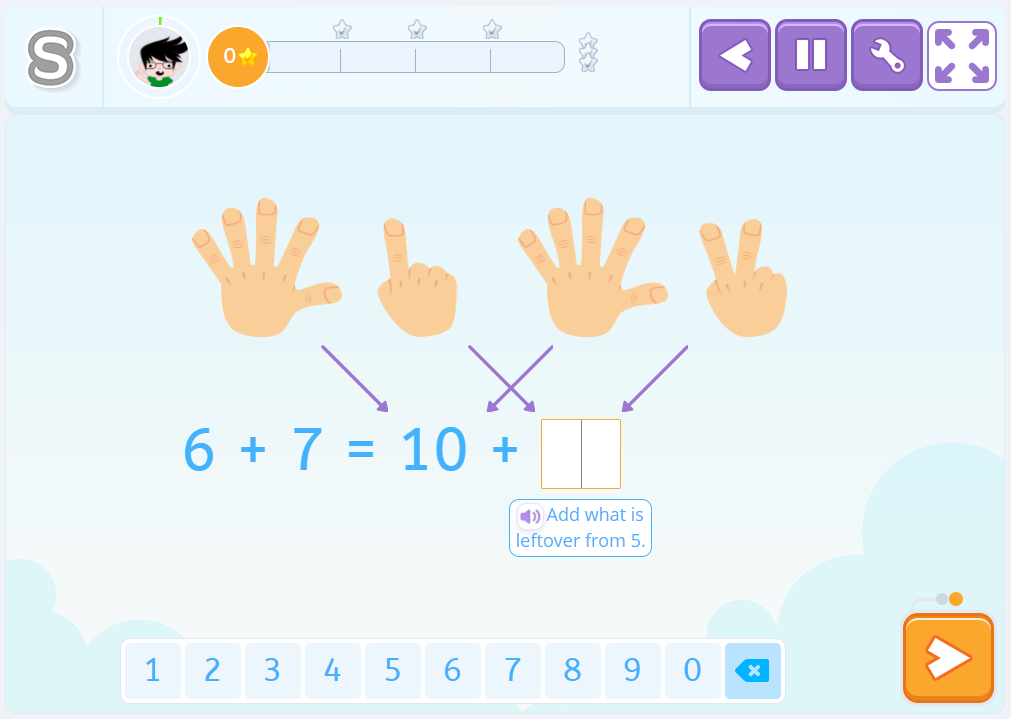
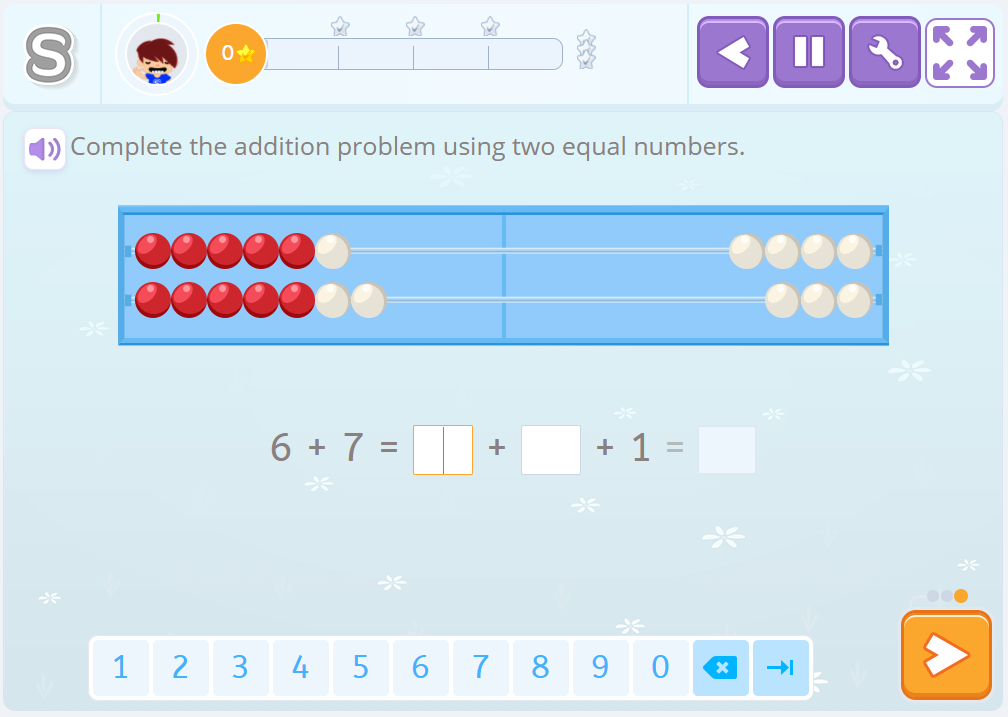
6+7
In order to solve this operation we break down 6 and 7 into addition problems based on 5, so 5 + 1 and 5 + 2. This breakdown is very common for children who use Smartick because they are familiar with the rekenrek. But most of us have counted on our hands before and therefore decomposition based on the number 5 is very popular.
So we are prepared to apply a very important numerical fact:
“Five and five is ten.”
Now we only need to add what is missing “the 1 for six” and “the two for seven”, which is 3. In other words, “ten plus three is thirteen.”
So, through decomposition of the addends, we have found operations that are much simpler for us because we have them internalized as numerical facts and have been able to solve the operation.
6+7 = 5+1 + 5+2 = 10 + 3 = 13
Other examples can implicate the use of doubles of numbers less than 10:
- Six and six is twelve; plus one, thirteen.
- Seven and seven is fourteen; minus one thirteen.
Jump Strategy
Jump strategies get their name because, although we apply bases of the decomposition of factors, we ‘jump’ down the number line. Let’s look at an example.
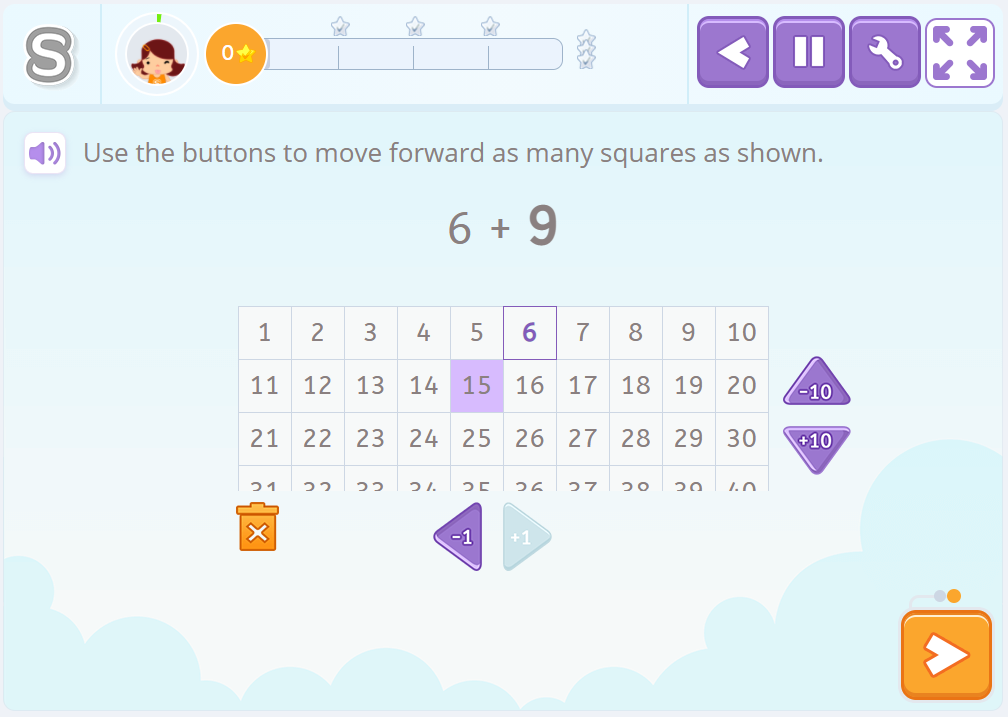
6+9
In these strategies, we usually use them as a reference, also the ten and multiples of five. So one way to solve this addition would be by stopping at the ten: “6 and 4, ten, and 5 that I have left to add, 15.”
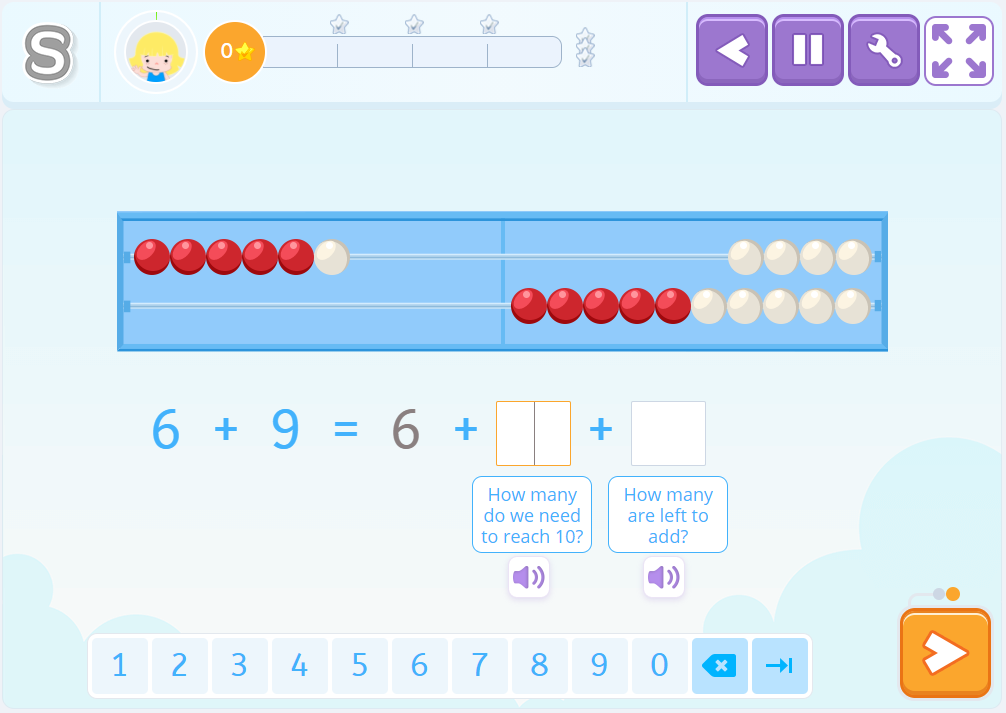
But we could also refer to how close the 9 of the ten is and calculate it like this: “9 plus 1 is ten, and 5 left to add, 15.”
Or fall back on the relationship that 9 has with ten and keep in mind that 9 is equal to 10 minus 1, that is, that adding 9 is the same as adding 10 and removing 1, or “add a ten and take away one unit.”
This is where our post on mental math strategies ends but there are many more to learn. Log on to Smartick and try it for free, so you can discover them all!
Learn More:
- Mental Calculation: Horizontal Addition and Subtraction
- Combined Operations: How to Solve These Types of Problems
- Strategies for Solving Incomplete Horizontal Additions and Subtractions
- Learn How to Perform Combined Operations
- Completing Additions, Subtractions, Multiplications and Divisions
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.
- Mathematical Formulas: What Are They, How Are They Made and Types of Formulas? - 11/29/2024
- The Language of Functions and Graphs - 07/01/2024
- Educational Technology: The Christodoulou Test - 05/06/2024
As I read through this post on math, I can’t help but be amazed at all the fascinating details I’m learning. Each new fact makes me even more excited to learn more about this topic. You’ve written so well that I feel like I could actually understand math now!
I know there are other great resources out there for learning math, so I’m going to check them out now. But before I go, I just want to say thank you for sharing all of this information with us. It’s really helped me understand math in a whole new way.