Addition and multiplication both use the associative property, while subtraction and division do not. We’re going to to get up close with each situation to get a better idea.
The associative property in Addition ♥
Addition indeed has the associative property.
Whatever numbers a, b, and c may be, they always end up the same:
(a + b) + c = a + (b + c) = (a + c) + b
Look carefully at the next example that’s set with actual numbers.
Let’s suppose that a=3, b= 18 and c=1. You already know to first calculate what’s in between parenthesis.
(3 + 18) + 1 = 21 + 1 = 22
3 + (18 + 1) = 3 + 19 = 22
(3 + 1) + 18 = 4 + 18 = 22
Just as you saw, regardless of the grouping order, the answer doesn’t change.
Now, I’m going to show you a more visual example:
We’re going to add 3 + 2 + 1, associating the numbers (grouping the fruits together) in two different ways.
First, looking at the top-left box in the picture above, we need to add the first two numbers, the 3 and 2. To whatever number comes out, 5, we’ll then add 1. We end up with 6. There are a total of 6 pieces of fruit.
In the picture to the right, we first add the last two numbers, the 2 and 1. 2 plus 1 gives us 3. After we add 3 to 3 and it gives us 6. There are a total of 6 pieces of fruit; it’s the same answer.
This is the associative property in addition: it allows you to change the order that we use to group the numbers because it doesn’t affect the final answer.
The associative property in Subtraction ×
Contrary to addition, subtraction doesn’t have the associative property.
Let’s look at another example. Let’s subtract 10 – 5 -3:
(10 – 5) – 3 = 5 – 3 = 2
10 – (5 – 3) = 10 – 2 = 8
If we subtract the first two numbers, 10 minus 5, it gives us 5. If we move on to subtract 3, it gives us 2. However, if we subtract the last two numbers first, 5 minus 3 is 2. If we subtract 2 from 10, it gives us 8.
Changing the way of associating the numbers in subtraction changes the answer. Thus, subtraction doesn’t have the associative property.
The associative property in Multiplication ♥
First, try to calculate (2 x 3) x 4. After, try 2 x (3 x 4). Did you get the same answer for both of them?
If you got the same answer, good job because multiplication has the associative property and the answer won’t change even if the number order of the problem changes. The order in which the numbers are associated doesn’t influence the final answer.
(a x b) x c = a x (b x c) = (a x c) x b
If a= 3, b= 5 y c = 10, we’re left with:
(3 x 5) x 10 = 15 x 10 =150
3 x (5 x 10) = 3 x 50 = 150
(3 x 10) x 5 = 30 x 5 = 150
Now, let’s take a look at how this property works with a more visual example:
We’re going to count the number of cubes that make up the following picture. There are 24 cubes in total.
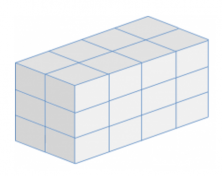
Other than counting each cube one by one, there are multiple ways to count the number of cubes.
One way is to first count the cubes in one column.
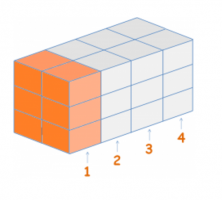
If we look carefully at the first column, that’s been colored orange, there are 3 x 2 = 6, 6 cubes. How many columns are there in total? There are 4 columns. So then, 6 times 4 will gives us the total number of cubes: 24 cubes.
Another way we can solve the problem is by counting the number of cubes there are in one row
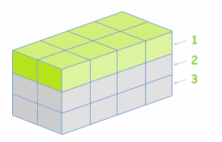
In the first green-colored row, there are 4 x 2 = 8 cubes. There are 3 rows in total, so in order to calculate the total number of cubes, we need to multiply 8 x 3, which comes out as 24. There are 24 cubes in total.
These are the operations that we used:
Regardless of how the numbers are grouped together, the answer comes out the same.
The associative property in Division ×
We’re going to calculate 8÷2÷2. First, try to divide (8÷2)÷2, what did you get? 8 divided by 2 is 4, and 4 by 2 is 2. Cool.
And now try 8 ÷ (2÷2). You need to work first on the parenthesis, 2 by 2 is 1 and 8 by 1 is 8. Nice. So, what are we seeing here?
We’re seeing that we got two completely different answers.
Let’s look at another example 18 ÷ 6 ÷ 3, grouping the numbers together again in two different ways and let’s test to see if the answer is the same or not.
One way gives us 1 and the other gives us 9. We see yet again that the answers are not the same.
So then, we can say confidently that division doesn’t have the associative property.
One thing before we end: if a problem doesn’t have parenthesis, you divide from left to right.
I hope this helped you to understand this important property. If you want to go deeper, you can visit these entries that we’ve posted on our blog:
And if you want to keep on learning more maths, at Smartick we teach them with jazz. Join us!
Learn More:
- How to Apply the Associative Property in a Problem
- What is the Associative Property of Multiplication?
- Applying the Commutative Property of Addition and Multiplication in a Problem
- Learn the Associative Property of Multiplication
- Learn about the Distributive Property of Multiplication
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.
- Mathematical Formulas: What Are They, How Are They Made and Types of Formulas? - 11/29/2024
- The Language of Functions and Graphs - 07/01/2024
- Educational Technology: The Christodoulou Test - 05/06/2024