The associative property states that the way in which factors are grouped together doesn’t affect the result of an operation:
(A x B) x C = A x (B x C)
Okay, so we know that the volume of a prism is calculated by multiplying the area of the base by the height: (B x C) x A u³ (cubic units).
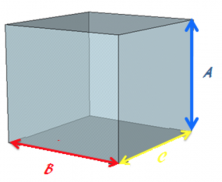
Let’s take a look at the associative property of multiplication with a concrete example.
Prism Side #1
So, we have a rectangular prism that is filled with water. If we calculate the quantity of water that we need in order to fill the prism, or in other words, the volume of the prism, we have:
Base=5 x 2
Height=10
Volume = (5 x 2) x 10 = 10 x 10 = 100
The rectangular prism’s volume is 100 u³.
Prism Side #2
Now, we’re going to calculate the same prism’s volume while it’s standing up on a different side:
Base = 10 x 5
Height = 2
Volume = (10 x 5) x 2 = 50 x 2 = 100
The volume is 100 u³, just like before.
Prism Side #3
Let’s go back to calculating the volume of this prism while it’s standing up one of its narrower sides:
Base = 10 x 2
Height = 5
Volume = (10 x 2) x 5 = 20 x 5 = 100
Once again, we find that it has a volume of 100 u³.
We’ve calculated the volume of the same prism using three different approaches and just as expected, we always ended up with the same volume.
So then, we see that the way of grouping numbers doesn’t affect the final answer of a problem with multiplication.
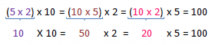
Isn’t the associative property of multiplication so easy?
If this post was helpful for you, pass it along to your friends! And if you want to learn more, subscribe to Smartick for free and have fun with math!
Learn More:
- Learn the Properties of Geometrical Prisms
- What Is a Prism? Solve These Exercises to Find Out
- Learn about the Distributive Property of Multiplication
- What is the Associative Property of Multiplication?
- Commutative Property in Multiplication and Addition
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.
- The Language of Functions and Graphs - 07/01/2024
- Educational Technology: The Christodoulou Test - 05/06/2024
- Multiplication Activities in Smartick - 04/09/2024