In this post, we are going to look at some sequenced examples of exercises with equivalent fractions. Remember that what we mean by equivalent fractions are those fractions that although they are different, represent the same quantity.
If you need to dig deeper into the concept take a look at this previous blog entry, examples of equivalent fractions.
The series of exercises that we explain below assume a sequence with which you will work in a very complete way with this type of fractions.
We begin with some activities with visual aids.
Complete the fraction so that they are equivalent fractions
- Find the numerator
As you can see, based on the graphic representations of the two fractions they are equivalent. You should find the missing numerator. In this case, it is enough to identify that the colored part of the fraction to the right is composed of 2 of 8 pieces.
So the missing numerator is 2.
- Find the denominator
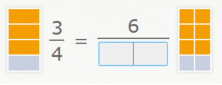
Again, focus on the graphic representations but this time you should find the missing denominator. Upon observing the fraction to the right, we see that the colored part represents 6 of 8 pieces.
Thus, the missing denominator is 8.
Calculate and obtain the equivalent fraction
Substitute the visual aid for the numerical reasoning between both fractions (x2).
- Obtain the equivalent fraction
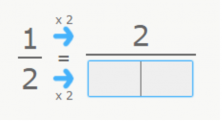
In this case, we are going to obtain an equivalent fraction by multiplying the numerator and denominator by the same number. We multiply 2 x 2 and obtain 4 (our denominator).
- Complete the original fraction so that they are equivalent
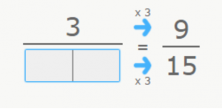
Now we deduce based on the previous exercise. We look for the number that multiplied by 3 gives us 15. 5 x 3 = 15.
The denominator we are looking for is 5.
Which fractions are equivalent to the representation in the image?
We add an image that helps us visualize the equivalencies:
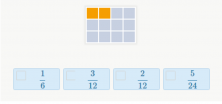In this exercise, you should choose the fractions that, between the options, are equivalent to the graphical representation.
You should choose 1/6 and the fraction that is represented in the image, 2/12.
Complete to make equivalent fractions
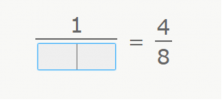
Finally, we have this exercise in which you should find, without any type of help, the denominator that makes these fractions equivalent.
In order to do this, we need to take note of the relationship between the numerators. What number multiplied by 1 gives us 4? (1 x 4 = 4)
After having identified said relationship, we should look for the number that multiplied by 4 gives us 8. (2 x 4 = 8).
In short, the denominator that we are looking for is 2.
We hope that with this sequence of exercises with equivalent fractions you now understand much better the concept of equivalent fractions.
If you want more practice problems with these, and much more, go to Smartick and register.
Learn More:
- Combining Decimals and Fractions
- Equivalent Fractions
- Do You Know What an Equivalent Fraction Is?
- Learn and Practice How to Find Sums of Fractions
- Subtracting Fractions Exercises with Common and Uncommon Denominators
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.
Thank you for your post. This really helped me explain to my great niece how to do fractions and since I´ve been out of school for so long it helped me also