In today’s post, we are going to see some examples of mass conversion problems with different units of mass and we will look at how to solve them.
Remember that previously, we have seen how to solve conversion problems with distance measures. Before beginning with the conversion problems with mass measures, you should review the principle mass measures by visiting the following post: Mass Measurement Problems
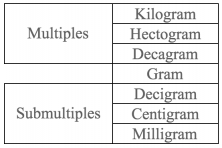
Let’s begin! First, take notice of the scale of the main units of mass measurement. You will be able to use them to help you with the conversions.
Three examples of Mass Conversion Problems

Sarah and Tony are twins. When they were born, Sarah weighed 600 grams more than Tony. A few days later their weights were equal due to Tony eating a lot. If Tony weighed 2.25 kilos at birth, then how much did Sarah weigh at birth?
In order to respond to the question, we must add both masses, but remember: we cannot add them just yet because they are expressed in different units.
In order to be able to add we are going to change the first part to kilograms. Notice on the scale: in order to change from grams to kilograms you have to move up. Therefore, we have to divide by 1,000:
1 kg = 1,000 g … then 600 g = 600 / 1000 kg … then 1,000 kg = 0.6 kg
Now we add:
2.25 kg + 0.6 kg = 2.85 kg
Thus, the answer to this problem is:
At birth, Sara weighed 2.85 kg.

Dani has two dogs: Jupiter is black and weighs 1,850 decagrams. The other dog, Romeo, is gray and weighs 24 kilos. Which dog is heavier? What is the mass difference between the two dogs?
In order to respond to the first question, we must compare the two masses. But we cannot compare them yet, because they are expressed in different units. Thus, the first thing that we must do is convert the first unit to kilograms:
From decagrams (dag) to kilograms (kg) you have to move up the scale and therefore, we have to divide:
1 kg = 100 dag … So 1,850 dag = 1,850/100 kg = 18.5 kg
Now, we can compare: Jupiter weighs 18.5 kg and Romeo weighs 24 kg. Thus, Romeo is heavier.
In order to respond to the second question, we must subtract:
24 kg – 18.5 kg = 5.5 kg
Therefore, the answer to this problem is:
Romeo is heavier, with a difference of 5.5 kg.

In order to make a chocolate cake, for every 0.5 kilos of flour, you have to add 100 grams of cocoa and a handful of nuts. Tomorrow, I am going to make a chocolate cake with 10 hg of flour. How much cocoa will I need?
This time, we have 3 different units of measurement. First, we will convert the decagrams (dag):
1 kg = 10 hg … 10 hg = 1 kg
If for every 0.5 kg of flour, we need 100 g of cocoa, for 1kg of flour, which is just double, we will need double the cocoa:
100 g x 2 = 200 g of cocoa
Therefore, the answer to this problem is:
You will need 200 g of cocoa.
What did you think of this post? Did it help you understand mass conversion problems with different measurements? If you want to practice more mass conversion problems, try Smartick for free!
Learn More:
- Mass Measurement Problems
- Learn How to Convert Mass Measures in the Metric System
- Learn about the Metric System and Measurements of Volume and Mass
- How to Solve Problems with Distance Conversions
- Conversion Capacity Problems in the Metric System







