In this post we will look at the properties of polynomials, what they are, what degree they have, and whether or not they complete and/or in standard form.
Let’s start by looking at what polynomials are.
A polynomial is an assembly of monomials.
Polynomials are usually named with capital letters (usually starting with the letter P) and the polynomial variables are written in parentheses.
P (a, b, c) = a 2 bc 3 – 3rd 3 c 6 + 6ac 4 + 2b
The polynomial P contains the variables a, b and c. It is composed of 4 monomials, therefore we can say that the polynomial has 4 terms.
Q (p, q) = -10p 6 + pq 2
The polynomial Q contains the variables p and q. It is composed of two monomials, therefore we can say that the polynomial has 2 terms.
Degree of a polynomial
The degree of a polynomial is the largest of the degrees of their monomials.
Let’s look at the degrees of the above polynomials:
The polynomial P has 4 monomials:
a2bc3 –> Degree =6
-3a3c6 –> Degree = 9
6ac4 –> Degree = 5
2b –> Degree = 1
Therefore, the degree of the polynomial P is 9.
The polynomial Q has two monomials:
-10p6 –> Degree = 6
pq2 –> Degree = 3
Therefore, the polynomial Q has a degree of 6.
What do you think is the degree of this polynomial?
Polynomials in Standard Form
A polynomial is in standard form when its monomials are ordered from largest to smallest degree.
Returning to the previous polynomials, the polynomial P has monomials of degree 6, 9, 5, and 1. As they are not ordered from largest to smallest, we can say that the polynomial P is not in standard form.
The polynomial Q has the monomials of degrees: 6, 3. In this case the degrees of the monomials are ordered from largest to smallest degree, therefore the polynomial Q is in standard form.
Is the following polynomial ordered?
Complete Polynomials
A polynomial is complete when you have all terms with degrees from the largest to the zero degree.
The polynomial P containing degrees 6, 9, 5 and 1 is incomplete, because terms of degree 8, 7, 4, 3, 2 and 1 are missing.
The Q polynomial is also incomplete because it has terms of degree 6 and 3, thus missing terms of degree 5, 4, 2, 1 and 0.
A final exercise: Is this polynomial complete?
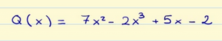
With this we have finished the post for this week.
To keep learning, register now for a 15-day Smartick free trial!
Learn More:
- Learn How to Add Polynomials with Examples
- Representing Polynomials with Algebra Tiles
- How to Subtract Polynomials with Help from Algebra Tiles
- Learn the Properties of Monomials
- Algebraic Expressions: What Are They? What Are They Used For?
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.
- The Language of Functions and Graphs - 07/01/2024
- Educational Technology: The Christodoulou Test - 05/06/2024
- Multiplication Activities in Smartick - 04/09/2024
I am a good student