In this post, we are going to continue analyzing the book How I Wish I’d Taught Maths by Craig Barton about evidence-based education. Today we are going to highlight the role that examples play in teaching mathematics and how to use them instead of mere definitions and instrumental rules.
Examples vs. Definitions
It is clear that concepts are the cornerstone of all forms of knowledge. The well-known Prussian philosopher Immanuel Kant claimed that the human experience is blind if there is no conceptual system with which to approach it. In mathematics, where (almost) everything is abstract, presenting a concept by its verbal definition tends to be considered the best way to present it. Thus, teaching something new is based on those definitions to make way for examples and practice.
Craig Barton presents us with some typical math definitions, starting with ”An equation is a statement that the values of two mathematical expressions are equal.” This definition is correct, but it assumes that we know what a ”statement” is, what a ”mathematical expression” is, and that we have a clear sense of when they are the same and when they are not.
For this reason, Barton proposes to use examples when introducing the concept.
The following expressions are equations:
- Y = X – 1
- Area = Base x Height
- 2X + 1 = 0
However, these are not:
- X
- X + 1
- X = 3 – 2X = 1
At Smartick we believe in the evidence-based methodology. As a result, we have developed activities like the following where students can work on the assimilation of concepts from chosen examples.

Examples vs. Rules
Something similar also happens with instrumental rules. In a math classroom, it is common to hear exclamations such as:
- “Two minuses make a plus.”
- “To find the mean you add up all the numbers and divide by however many numbers there are.”
- “Subtraction cancels out addition.”
These rules may seem beneficial in the short term because they obviously produce a sense of improvement and know-how. However, they do not imply, under any circumstances, a deep understanding of the concepts. Furthermore, in Skemp’s words, the student who only knows instrumental rules would outright fail if the teacher did not ask something that did not fit perfectly into those rules.
In this way, current teaching methodologies are strongly committed to turning their attention to the ideas behind the rules. Using context to interpret and provide direction, helping students make sense of what they are doing. For example, at Smartick we work the usual rules of solving equations within the context of scales.
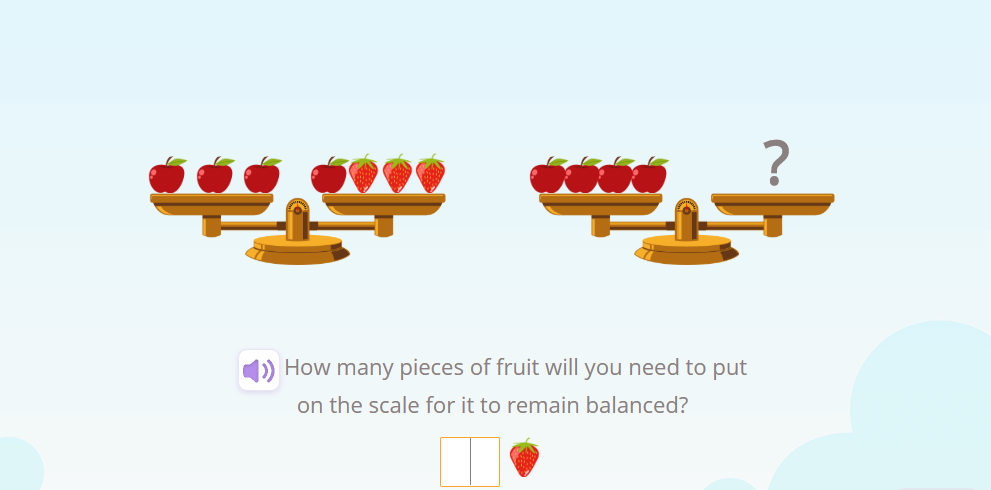
On the first scale, we can see that there are three apples that weigh the same as one apple and three strawberries. In algebraic language, X represents each apple and Y represents each strawberry, so this can be expressed as 3X = X + 3Y. The cancelation rule now makes perfect sense because if we remove an apple from each plate, the scale will remain balanced.
If you would like to go beyond instrumental rules and truly understand mathematics, join the Smartick community. Click here to register for free!
References
- Barton, Craig. How I Wish I’d Taught Maths: Lessons Learned from Research, Conversations with Experts, and 12 Years of Mistakes, 221-260. Melton, Woodbridge: John Catt Educational, 2018.
- Skemp, R.R. (1976) “Relational understanding and instrumental understanding”, Mathematics Teaching 77 (1) pp 20-26
Learn More:
- Worked Examples and Metacognition
- Diagnostic Questions in Mathematics Education
- Learning with Analogies. Are Analogies Good for Learning?
- Motivation – Evidence Based Education
- Algebraic Expressions: What Are They? What Are They Used For?







