Aug12

Representing Powers with Rods

In today’s post, I am going to show you how to represent powers with rods. It is fun and easy, you’ll see!

We will represent powers to the 2nd and 3rd degree, which are the ones we can reproduce within three dimensions of the physical world.

To begin, I will show you a picture of the rods that represent each number from 1 to 10:

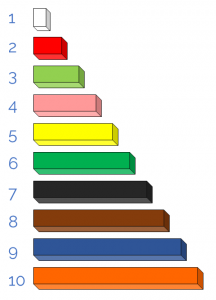
powers

If you would like to download them and use a paper version of the rods, you can do so here.

Now let’s look at 2nd-degree powers.

2nd Degree Powers: square numbers

We are going to represent the following power:

Since four squared is four multiplied by four:

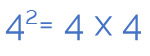
In order to represent it with the rods, we use the number four rod four times.

We can do so by forming a square, putting each one on top of the other.

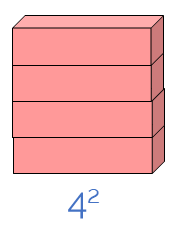
powers

This way we have represented the power of four squared, or ”the square of four,” which is 16 in the form of a square: 4 units wide and 4 tall.

In the same way, we can represent the squares of numbers 1 to 10 in the form of a square:

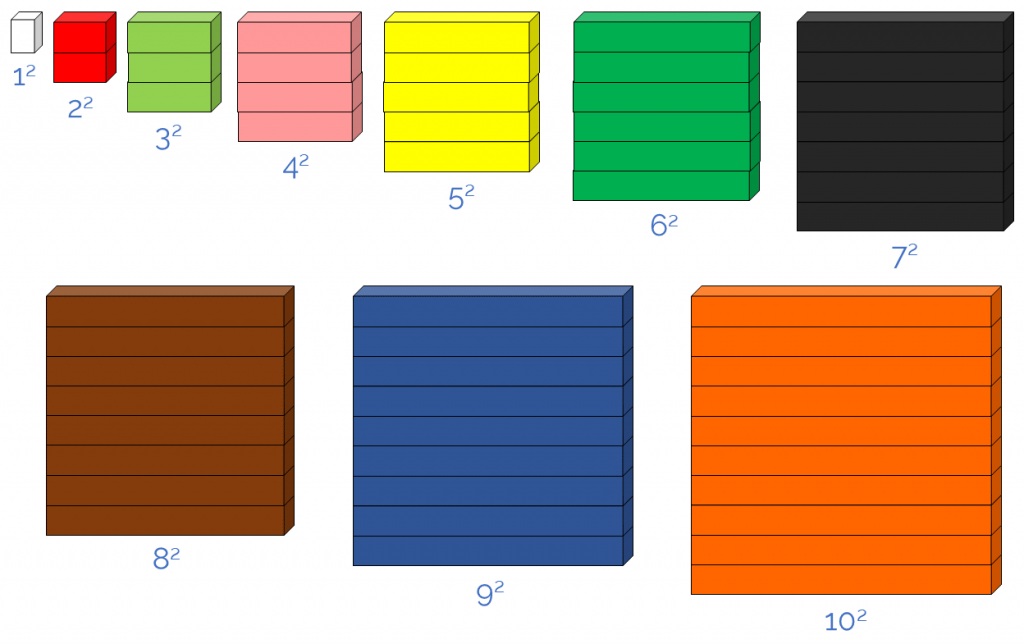
Since each power is to the 2nd degree they can be represented in the shape of a square. These numbers are called square numbers (1, 4, 9, 16, 25, 36, 49, 64, 81, 100, …). Did you know that?!

Now let’s see powers to the 3rd degree!

3rd Degree Powers: cubed numbers

Continuing with the number 4, we are going to represent the following power:

Since four cubed is four multiplied by four 3 times:

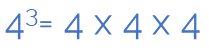
And since we have already represented four squared, it will be just as easy representing four cubed(remember that its front part was square?) because it’s repeated four times.

If we put each representation of four squared one behind the other, we’ll have formed a cube:

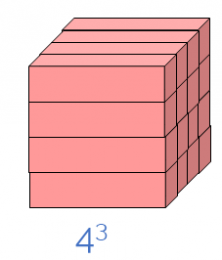
powers

So we have represented the power of four cubed, or ”the cube of four,” which is 64 in the shape of a cube, 4 units wide, 4 deep, and 4 tall.

Similarly, we can represent the cubes of the numbers 1 to 10 in the shape of a cube:

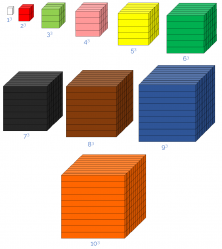Since each 3rd-degree power can be represented in the shape of a cube, these numbers are called cubic numbers (1, 8, 27, 64, 125, 216, 343, 512, 729, 1.000, …).

Well, there you have it, representing powers with rods!

Do you know about the squared numbers? And cubic? Tell us in the comments!

And as you already know, if you would like to continue learning mathematics topics like this, login to Smartick and try our method for free.

Learn More:

Fun is our brain’s favorite way of learning

Diane Ackerman

Smartick is a fun way to learn math

15 fun minutes a day
Adapts to your child’s level
Millions of students since 2009

Author
Recent Posts

Smartick

Content Creation Team.
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.