Sometimes we may be interested in knowing if one number is divisible by another, without having to perform a division. This is especially useful when we work with large numbers that require a lot of time for completing calculations. If you would like to refresh your memory on divisibility criteria, take a look at this previous post.
However, in this post, we will go further and explain the reasoning why divisibility criteria work. So, let’s go!
The fundamental idea of divisibility is the notion of the remainder. When we divide, we start with a complete set that has a number of elements (dividend) and group them together into smaller subsets, all with the same number of elements (divisor). The remainder is formed by the elements that ”are leftover” when we can no longer make groupings. You can review division here. Thus, the remainder is always less than the divisor. Otherwise, we would be able to continue to make groupings. For example, if we are dividing by 3, the remainder can only be 0, 1, or 2.
The remainder of dividing by any number must always abide by certain properties. Among them, we are interested in two — if a and b are any two whole numbers, then:
- remainder of ( a + b ) = ( remainder of a ) + ( remainder of b )
- remainder of ( a x b ) = ( remainder of a ) x ( remainder of b )
Make sure that the criteria are met!
On the other hand, when we have a number, we can always write it according to its decimal representation. For example, if we have AB, a 2 digit number, we can express it as:
AB = A x 10 + B
By taking into consideration the properties of the remainder, we must calculate:
remainder of ( AB ) = ( remainder of A ) x ( remainder of 10 ) + ( remainder of B )
What happens now is that, if we know the remainder of each of the digits (A, B) and the remainder of 10, we can find the remainder of the original number. Furthermore, we can do so in order, from left to right, in the previous operation. First, we use the remainder of A,
( remainder of A )
then we must multiply by the remainder of 10,
( remainder of A ) x ( remainder of 10 )
and after that, we must add the remainder of B,
( remainder of A ) x ( remainder of 10 ) + ( remainder of B )
In order to understand this better, let’s make a graph that allows us to show the previous example visually with a specific number. For example, we can use the remainder of dividing by 7. We could have chosen another number, but… we like 7!
Then the possible remainders are then 0, 1, 2 3, 4, 5, and 6. They will continue repeating themselves in that order. In fact, the result of 7 divided by 7 is 0, 8 divided by 7 is 1, 9 divided by 7 is 2…
First, we place the possible remainders at the vertices of a heptagon (a 7-sided figure). Then, we join them with blue arrows oriented in the direction that the remainders are occurring. Now, with purple arrows, we join each of the remainders with the remainder of the number that is the result of multiplying it by 10. For example, 3 is joined to 2 with a purple arrow, as 3 x 10 = 30 and the remainder of dividing 30 by 7 is 2. With this information, we have obtained the following graph:
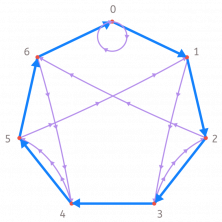
The method above means that starting from 0, we have to go through as many blue arrows as indicated by the first digit of the number (starting from the left), and then go through a purple arrow. Then, we must do the same with the next digit.
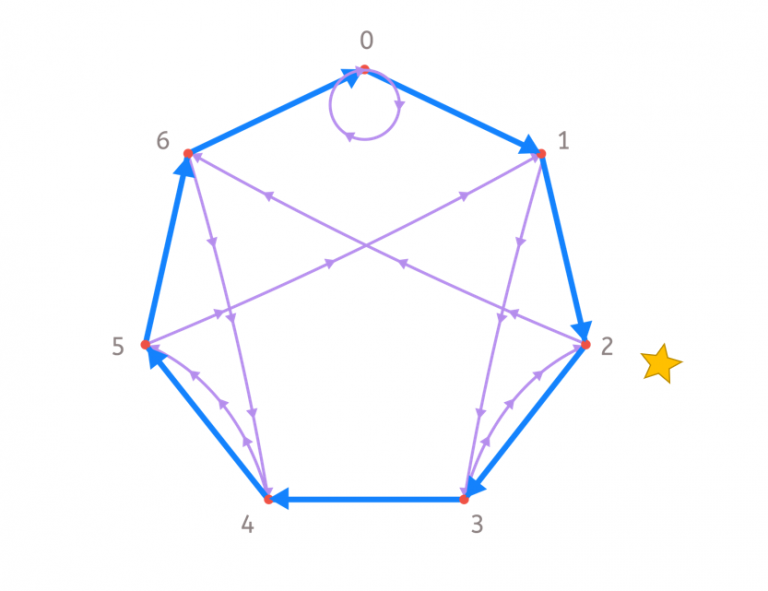
For example, let’s see if the number 91 is divisible by 7. First, we follow 9 blue arrows, starting from 0.
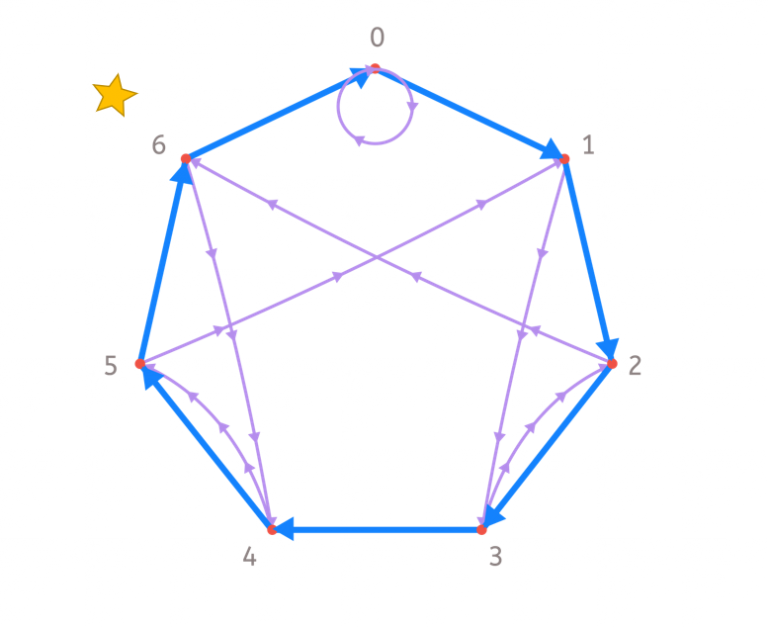
Now, we follow a purple arrow and we stop at 6.
Since the next digit is a 1, we go through 1 with a blue arrow and arrive at 0. Be careful though! If the digit is the last one, we no longer have to go through the purple arrow! Thus, we come to:
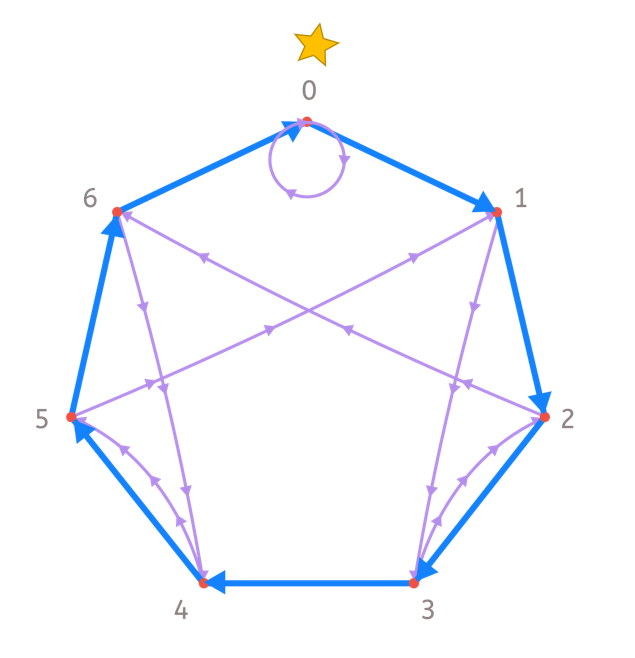
Since we have ended up at 0, we know that the remainder of dividing 91 is 0. In other words, 91 is divisible by 7. Check it!
This way of viewing divisibility criteria is helpful for numbers made up of more digits. Just follow the path of blue and purple arrows correctly to know if a number is divisible by 7. In addition, you can make your own graph for any number you want, and thus you will get your own criteria of divisibility. Next, you can see the criteria for number 3. In this case, we use a triangle because it has 3 sides. Note that the purple arrows always go to the same vertex. That means that what really matters is where you end up if you take as many steps as the sum of all the digits. Does that remind you of the divisibility criteria of 3?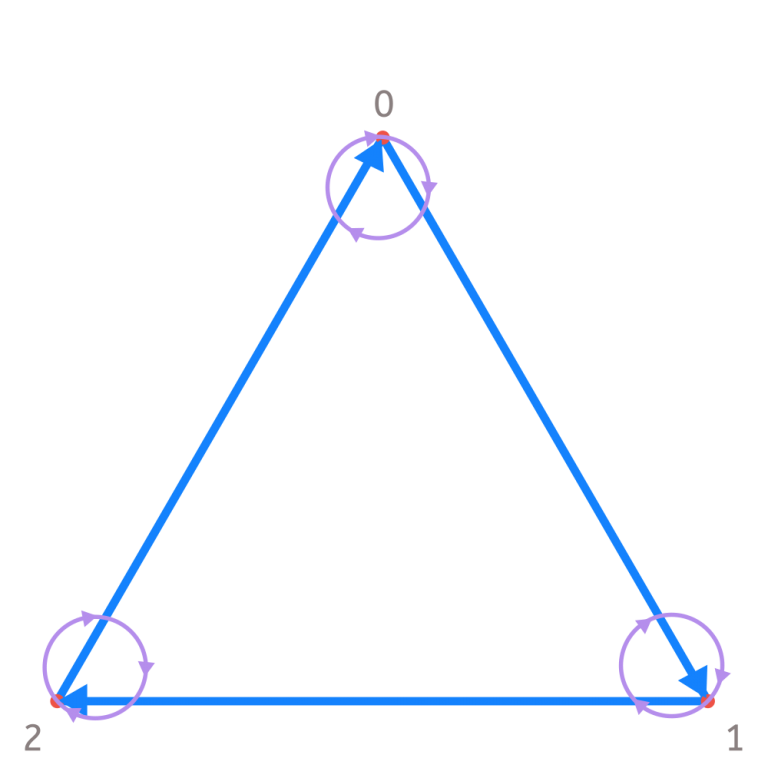
I am also going to show you the graph for the number 5 (with a pentagon, a 5 sided figure). All of the purple arrows are going to stop at 0 because any number multiplied by 10 is divisible by 5. Therefore, the only thing that matters is what happens to the last digit. We end up with 0 only if the last digit is 5 or 10. This is the divisibility criteria of 5!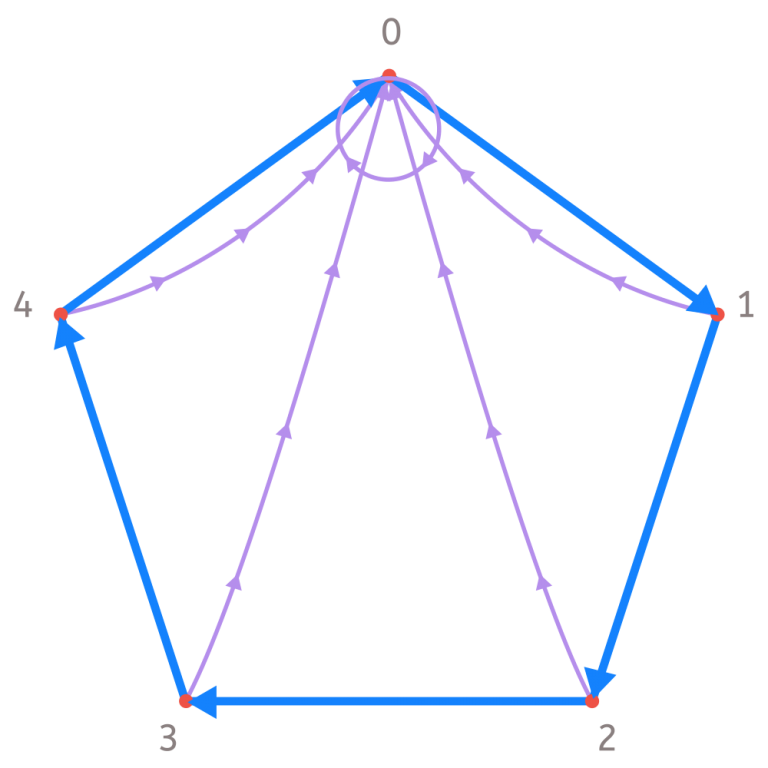
Why don’t you try developing the criteria of divisibility by, for example, the number 13? 
I hope that you have expanded your knowledge about the criteria of divisibility and that now you understand how it works. If you would like to keep learning about more topics like this, join the Smartick community! Try it for free!
Learn More:
- Divisibility by 4: How Do We Know If a Number Is Divisible by 4?
- Divisibility Criteria for 3, 4, 9 and 11
- Follow the Divisibility Guidelines for 3
- Divisibility Guidelines for 6 and Some Examples
- Divisibility Guidelines for 5 and Some Examples
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.
- Mathematical Formulas: What Are They, How Are They Made and Types of Formulas? - 11/29/2024
- The Language of Functions and Graphs - 07/01/2024
- Educational Technology: The Christodoulou Test - 05/06/2024