In this post, we are going to justify, in a pedagogical sense, the conceptual base of the commutative property and it’s most basic and practical applications.
The first thing we need to do is review the concept of the commutative property. For this I have linked some older blog posts about this topic:
- Applying the Commutative Property of Addition
- Properties of Multiplication
- Commutative Property in Multiplication and Addition
- Addition Properties with Examples
After reviewing these posts, we can start with the new material.
Being able to switch (change the place of) the terms involved in an addition or multiplication problem allows the exercise to conserve our efforts. This is because it is easier to do the calculation in one direction than another.
With these two examples, you will be able to perfectly understand the importance of this property for the learning and development of mathematics in primary school.
Commutative Property of Addition
Generally, any small child with their first addition problems finds it easier to start with the smaller number and add the larger one to it. With the passing of time, some part of this stays with us. For example, when we are in a situation where we need to add 9 people to the invite list for a party, which already has 3 confirmed guests, we unconsciously change the situation and switch the digits. So, instead of adding 3+9, we optimize our cognitive resources and perform the operation backward, 9+3, applying the commutative property without even knowing it.
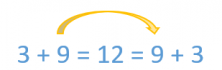
Commutative Property of Multiplication
By memorizing multiplication tables we also welcome the commutative property of multiplication to ”cross” the combinations of factors that we already know and use them as guides in more complex tables. The clearest example of all the combinations of the table is 5. Once this table is memorized, swap their products, and it clearly helps us to solve the tables of higher numbers. (5×7 for 7×5, 5×8 for 8×5, 5×9 for 9×5… )
There are infinite examples of situations like these that demonstrate the importance of this property. Can you think of other situations where we use it as a resource to conserve our efforts?
Don’t hesitate to write your answer to my question on this thread and don’t forget that you can try our method for free by logging into Smartick.
Learn More:
- Learn the Different Properties of Multiplication
- Applying the Commutative Property of Addition and Multiplication in a Problem
- Review the Different Properties of Multiplication
- Some Tricks to Make Times Tables Shorter
- Multiplication Tables and Tricks to Learn Them
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.
- The Language of Functions and Graphs - 07/01/2024
- Educational Technology: The Christodoulou Test - 05/06/2024
- Multiplication Activities in Smartick - 04/09/2024