In today’s post, we’re going to learn two basic concepts of statistics: average and median.
Imagine if we asked all of our classmates what grade their math grade was for this marking period. Assuming that there are 25 people in our class, we’ll collect 25 numbers:
It’s a little complicated to process the numbers if they’re jumbled like that, right? What would be the first thing you’d do with these numbers? I’d put them in order.
Now, let’s take a closer look at a few things: a lot of my classmates got 5s or 6s:
…and assuming that we needed a 5 to pass, only 7 students failed.
There are plenty of questions that we could ask ourselves regarding the information that we have on the class’ grades. The first question usually is: did the class get high grades in math or was that not the case? How can we know? We can know by looking at the average grade of the class.
Average
In order to make a summary of a group of numbers, we use an average—I’m sure that you’ve heard of it before! To find the average, we have to follow the steps below:
- Count the total numbers that we have. In this example, we are working with 25 numbers.
- Add the numbers.
- Divide the sum by how many numbers we have.
So then, the average grade is 5.6. What does this mean? It means a lot of things:
- It means that, in general, the class grades are around 5.6.
- It means that it’s a normal class; I have classmates that passed with high grades and others that failed, but it’s balanced.
But what’s important is that instead of repeating all of the class grades again, we can simply say that the average grade is 5.6.
Let’s imagine now that a new student comes to class. We don’t know what grade he or she will get, so what do you think will happen to the average?
- If the new student gets a 0, the average will be:
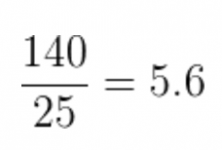
- If the new student gets a 5, the average will be:
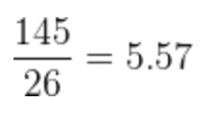
- And if the new student gets a 10, the average will be:
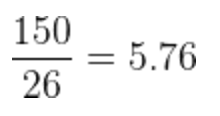
Observe how if the new student gets a 5, the grade is pretty close to the average that we had before, so the new average almost doesn’t change! But if the student gets a 0 or a 10, a grade that’s further away from the old average, the new average changes two decimal points!
So, the average changes a lot when it has to account for a number that’s really far away from it. In order to avoid a huge change in the average, we could use another similar tool: the median.
Median
In order to avoid being thrown off by an altered average, we’re going to find out how to find the median.
The first thing we need to do (if we haven’t done it already) is put the numbers in order.
And now we need to find the number that’s in the middle:
That’s the median!
Now, let’s find the median in three different situations. We have 26 numbers to work with now, meaning that there is no number in the middle, so we need to find the average of the two numbers that are in the middle.
- If our new classmate gets a 0…
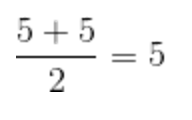
- If our new classmate gets a 5…
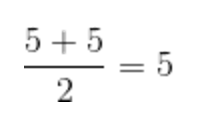
- If our new classmate gets a 10…
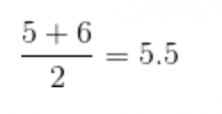
As you can see, the median only changed when the new classmate got a 10. It’s actually a coincidence because normally, the median doesn’t change much when accounting for outliers…but “most of the time” doesn’t mean “always!”
Was this post about finding the average and median helpful to you? Share it on your social media and try out Smartick for free.
Learn More:
- Adding Strategy for Numbers That Are One or Two Values Apart
- Commutative Property in Multiplication and Addition
- No More Homework? A Texas Teacher’s Letter Goes Viral
- How to Evaluate Number Sequences
- How to Solve Problems with Distance Conversions
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.
- Mathematical Formulas: What Are They, How Are They Made and Types of Formulas? - 11/29/2024
- The Language of Functions and Graphs - 07/01/2024
- Educational Technology: The Christodoulou Test - 05/06/2024