The pedagogical and parents customer service team at Smartick often receive questions from parents whose children have said they are confused because at school they learn subtraction one way and Smartick teaches them another.
At Smartick we feel that the use of one algorithm or another doesn’t matter, what’s important is that it is explained in a comprehensive way to help students fully grasp the concepts.
In today’s post, we are going to see the differences that exist between two subtraction algorithms with borrowing: by compensation and by regrouping.
We are going to see what each algorithm consists of.
Subtraction with borrowing by compensation
This algorithm for subtraction with borrowing is what is traditionally used in Spain, ”I take 1”, inherited without much sense from the algorithm of addition with borrowing.
It consists of adding the same amount to the minuend and the subtrahend (in this case,10 units to the subtrahend and 1 ten to the minuend).
By doing this, the difference is maintained and we get enough units in the minuend to subtract units from the subtrahend.
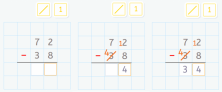
The calculations are as follows:
72 – 38 = (72 + 10) – (38 + 10) = (70 + 12) – (40 + 8) = (70 – 40) + (12 – 8) = 30 + 4 = 34.
At Smartick we think that reasoning is artificial and difficult for children in first and second grade to understand, so we prefer to not use this algorithm in our activities.
Subtraction with borrowing by regrouping
This algorithm has become more popular in recent years and is relatively unknown to some parents who try to help their children with their homework and learn about this different way to solve subtraction with borrowing.
It consists of taking a ten from the subtrahend and breaking it down (decomposing) into 10 units in order to have enough units to subtract from the minuend.
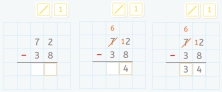
The calculations are as follows:
72 – 38 = (60 + 12) – (30 + 8) = (60 -30) + (12- 8) = 30 + 4 = 34.
Decompositions of the numbers involved are made without introducing amounts in an artificial way. In Smartick we use this algorithm because it is more natural and easier for students to assimilate in first and second grade.
We will use base 10 blocks to help us understand better and look at the earlier example in steps, you’ll see how easy it is!
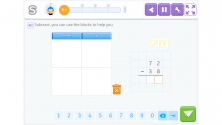
The first thing we will do in represent the minuend, 72, with blocks:
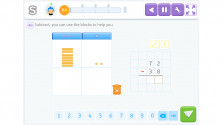
Since we do not have enough units in the minuend to subtract the 8 units from the subtrahend, we take a ten from the minuend and move it to the units:
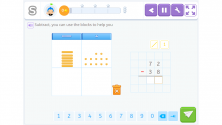
We have 12 units, enough to subtract 8. 12 – 8 = 4 units.
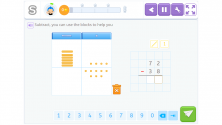
Now, we can subtract 3 tens from the subtrahend:
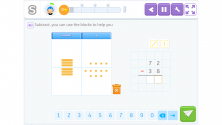
So we have the answer to the subtraction problem! Subtracting 38 units from 72 leaves us with 34 units.
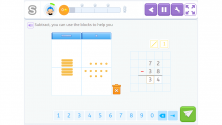
Now you have seen the difference between these two algorithms for subtraction with borrowing. I hope it has helped you to have a better understanding.
If you would like to continue learning primary mathematics, login to Smartick and try it for free.
Learn More:
- How to Solve a Subtraction Problem with Regrouping
- Mental Calculation: Horizontal Addition and Subtraction
- Subtraction With and Without Carrying
- Learn How to Subtract without Regrouping
- Mental Calculation Strategies: Add and Subtract Numbers
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.