In this post, we are going to learn how to calculate a half, third, fourth, and fifth. These expressions are not just used for math problems, but also in daily life!
Do you know what they are? Do you know how to calculate them? You are going to see how easy it is to calculate a half, third, fourth, and fifth.
The expressions “one half”, “one third”, “one fourth” or “a quarter”, and “one fifth” are fractions that are often used in our daily lives. We use them when we are referring to elements that are, or can be, divided into equal parts.
Index
A Half
Do You Know What a Half Is?
A half is equivalent to the fraction \(\frac{1}{2}\), therefore it is half of an amount and can be calculated by dividing by 2.
We also hear it outside of mathematics, “I have half a sandwich.”

How to Calculate a Half
Calculating a half is dividing by two, that’s why a half an hour is 30 minutes because it is 60 divided by 2.
If we have several halves, for example, four halves of 18 = \(\frac{4}{2}\) de 18, you have to do the following:
- First, you need to divide 18 by 2, which is 9.
- Then, you multiply the numerator of the fraction (4) by 9, the result of the previous division.
- And we are left with the multiplication 4 × 9 = 36.
Examples: Half
Half of 10 = \(\frac{1}{2}\) of 10 = \(\frac{10}{2}\) = 5
Half of 34 = \(\frac{1}{2}\) of 34 = \(\frac{34}{2}\) = 17
Half of 14 = \(\frac{3}{2}\) of 14 = 3 × \(\frac{14}{2}\) = 3 × 7 = 21
A Third
What is a Third?
A third is equivalent to the fraction \(\frac{1}{3}\), therefore it is one-third of an amount.
There are many examples of thirds in daily life, such as “You’ve eaten a third of my chocolate bar!”
![]()
How to Calculate a Third
If you want to calculate several thirds of some amount, for example, six-thirds of 24 = \(\frac{6}{3}\) of 24, you need to do the following:
- First, you need to divide 24 by 3, which is 8.
- Then, you multiply the numerator of the fraction (6) by 8, the result of the previous division.
- And we are left with the multiplication 6 × 8 = 48.
Examples: Third
A third of 24 = \(\frac{1}{3}\) of 24 = \(\frac{24}{3}\)= 8
A third of 33 = \(\frac{1}{3}\) of 33 = \(\frac{33}{3}\) = 11
Five thirds of 15 = \(\frac{5}{3}\) of 15 = 5 × \(\frac{15}{5}\) = 5 × 5 = 25
A Fourth
What is a Fourth?
A fourth is equivalent to the fraction \(\frac{1}{4}\). A fourth is one-quarter of an amount when it is divided by 4. I’m sure, one time or another, you have told time by saying, “It is quarter past 12.” As you know, a quarter of an hour is one-fourth of 60 minutes (60/4 = 15), 15 minutes.

How to Calculate a Fourth
In order to calculate fractions of amounts that have four as a denominator, for example, nine-fourths of 36 = \(\frac{9}{4}\) of 36, you need to do the following:
- First, you need to divide 36 by 4, which is 9.
- Then, multiply the numerator of the fraction (9) by 9, the result from the previous division.
- And we are left with the multiplication 9 × 9 = 81.
Examples: Fourth
A fourth of 20 = \(\frac{1}{4}\) of 20 = \(\frac{20}{4}\) = 5
A fourth of 28 = \(\frac{1}{4}\) of 28 = \(\frac{28}{4}\) = 7
Seven fourths of 8 = \(\frac{7}{4}\) of 8 = 7 × \(\frac{8}{4}\) = 7 × 2 = 14
A Fifth
What is a Fifth?
A fifth is equivalent to the fraction \(\frac{1}{5}\), therefore fifths are one-fifth of an amount and are calculated by dividing by 5. You may be familiar with the phrase ‘pleading the Fifth’, which refers to the Fifth Amendment of the United States Constitution.

How to Calculate a Fifth
Calculating a fifth of something is very easy, you just need to divide by 5.
If you need to calculate several fifths, for example, ten-fifths of 55 = \(\frac{10}{5}\) of 55, you need to do the following:
- First, you need to divide 55 by 5, which is 11.
- Then, you need to multiply the numerator of the fraction (10) by 11, the result of the previous division.
- And we are left with 10 × 11 = 110.
Examples: Fifth
A fifth of 40 = \(\frac{1}{5}\) of 40 = \(\frac{40}{5}\) = 8
A fifth of 10 = \(\frac{1}{5}\) of10 = \(\frac{10}{5}\) = 2
A fifth of 35 = \(\frac{3}{5}\) of 35 = 3 × \(\frac{35}{5}\) = 3 × 7 = 21
Problem: Halves, Thirds, and Fourths
Annie, Pete, and Veronica went to the supermarket yesterday. Each one of them bought one dozen eggs because they were on sale. When they got home, Annie made an omelet using one-third of her dozen eggs, Pete made scrambled eggs with half of his dozen, and Veronica used one-fourth of her dozen to make a cake. How many eggs did they each use?
First, we need to remember that one dozen eggs is 12 eggs. Now, let’s look at the information we have:
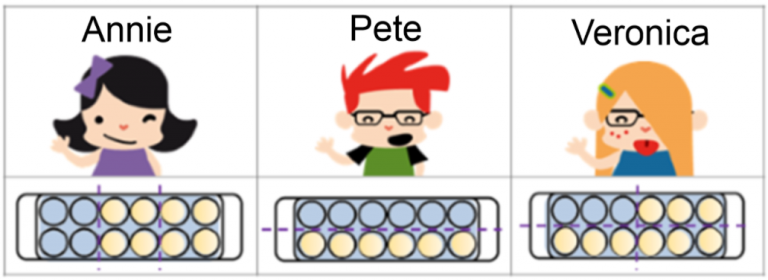
- Annie used a third of her dozen eggs. If we look at the picture we can see that the dozen is divided into three equal parts and she has used one of these parts, in other words, 4 eggs. We can calculate it by dividing 12 / 3 = 4.
- Pete used half of his dozen eggs. If we look at the picture we can see that the dozen is divided into two equal parts and he has used one of these parts, in other words, 6 eggs. We can calculate it by dividing 12 / 2 = 6.
- Veronica used one-fourth of her dozen eggs. If we look at the picture we can see that the dozen is divided into four equal parts and he has used one of these parts, in other words, 3 eggs. We can calculate it by dividing 12 / 4 = 3.
Problem: Fifths
In order to fill a swimming pool, a water truck came and emptied three-fifths of its tank, which contains 18,000 liters of water. How many liters of water were put into the pool?
- We need to calculate \(\frac{3}{5}\) of 18.000.
- We divide 18,000 by 5, which is 3,600 liters (this is a fifth of the tank, but the pool used 3).
- We multiply 3,600 by 3, which is 10.800 liters, let’s swim!
What did you think? If you found this post useful, share it with your friends!
And if you would like to learn more about elementary mathematics register for free with Smartick!
Learn More:
- Learn about Fractions: Halves, Thirds and Fourths
- Learn How to Calculate Halves, Thirds and Fourths
- How to Simplify Fractions with Examples
- Subtracting Fractions Exercises with Common and Uncommon Denominators
- Understand What a Fraction Is and When It Is Used








to study my child a math she is in grade 6
Hello Ncammy,
Thank you very much for your comment.
If you want your child to learn more content like this and practice elementary math, all you have to do is sign up for Smartick. You have a free trial period with no obligation.
If you have any additional questions or doubts you can write to my colleagues in the pedagogical team at [email protected].
Best regards!