In today’s post, we are going to work with the Rule of Three, direct or inverse, by looking at some sample problems. If you want, before we begin, you can review how to use the Rule of 3.
First of all, we are going to see what is the difference between the Direct Rule of Three (DIrect Proportion) and the Inverse Rule of Three (Inverse Proportion):
Direct Rule of Three = Direct Proportion
- When increasing one quantity, the other increases in the same proportion.
Inverse Rule of Three = Inverse Proportion
- When increasing one quantity, the other decreases in the same proportion.
Now that we’ve cleared up what the Rule of Three for Direct and Inverse Proportion are, let’s take a look at some problems to understand it better.
Direct Rule of Three Problems
Today we are going to go on a school excursion and we need to make sandwiches for the whole class. If we need 2 loaves of bread to make sandwiches for my 4 siblings, how many loaves of bread will we need in order to make sandwiches for all 24 students in the class?
The first step is to determine if we need to use the Direct Rule of Three or Inverse Proportion:
- If we make more sandwiches, will we need more loaves of bread?
- Any time that we make more sandwiches, we will need more bread.
So that means that as one quantity increases, the other increases in the same proportion: this problem requires the Direct Rule of Three.
Once we know what kind of problem we are dealing with, we can go ahead and solve it:
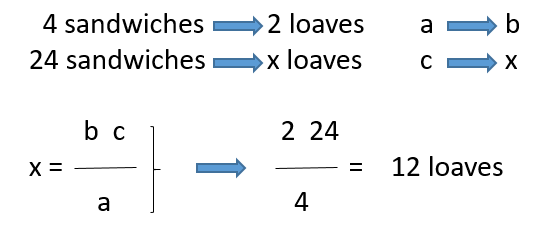
Answer: We will need 12 loaves of bread to make sandwiches for 24 students.
Inverse Proportion Problems
Last month, it took 3 gardeners 12 hours to fix up the gardens in the city’s main square. This month, the city has a bigger budget and can hire 6 gardeners. Knowing that it took 12 hours to finish the job for 3 gardeners, how much time will it take for 6 gardeners to fix up the gardens?
The first step is to determine whether the problem requires the Direct Rule of Three or Inverse Proportion:
- If the city hired more gardeners, will it take more or less time to finish the job?
- Having more gardeners will reduce the total time of work.
So, as one quantity increases, the other decreases in the same proportion: we are solving an Inverse Proportion problem.
Once we know what kind of problem we are dealing with, we can go ahead and solve it:
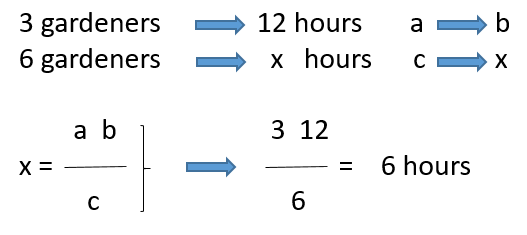
Answer: With 6 gardeners, the gardens will be fixed up in 6 hours.
What did you think about this post? Did it help you understand the Rule of Three problems? If it helped, share it with your friends. And if you want to learn much more elementary math, try Smartick for free.
Learn More:
- Problems Involving the Inverse Rule of 3
- Inverse Proportionality: The Rule of Three Inverse
- Rule of 3: Direct and Inverse
- Compound Rule of 3: When to Use It and Some Problems
- Inverse Proportionality: What Is It?
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.
- Mathematical Formulas: What Are They, How Are They Made and Types of Formulas? - 11/29/2024
- The Language of Functions and Graphs - 07/01/2024
- Educational Technology: The Christodoulou Test - 05/06/2024
This is fantastic!
Do the kids work on this on the App? I just tried looking for the video tutorial for this on the app and couldn’t find it, it should be under fraccions, right? Or may e under algebraic expressions as they start working with “x”?
Thank you very much for your comment Gema!
The children work on this content in their learning sequence in Smartick, we don’t have it in tutorial form, but the children will be able to learn it with guided exercises as they go along in Smartick.
Best regards!
The explanations are easy to understand. Thanks Smartick.
Thanks so much.. This explanation helped greatly.
I really love the explanation, it helped me a lots. Thanks smartick.
Hey guys, I really enjoyed the post. Thank you very much for a job so well done ! Continue to inspire more millions of elementary learners , and may you be in good health !
No. Question 2 should be x= (6 x 12 )/ 3 = 24 hours .
Hi Hayden:
This is the Inverse Rule of Three, since the ratio is the reverse: the more gardeners work in the garden, the less time it will take to fix it. It does not make sense that 3 gardeners take 12 hours and 6 gardeners take 24 hours. Therefore, the correct formula to be used is: (3 x 12) / 6 = 6. Double the gardeners will take half the time to do the same work.
Thanks!