In this week’s post, we’re going to look at what the rule of three inverse is and how to use it to solve problems.
The rule of three is a way to solve proportionality problems. If we are dealing with a direct proportionality, then apply the direct rule of three. If we are dealing with inverse proportionality, we apply the rule of three inverse.
Let’s take a look at what inverse proportionality is so that we can see learn how to apply it later on in this post.
What is Inverse Proportionality?
We have 2 magnitudes (A and B) and we need to observe the relationship that exists between the two. In order for the inverse proportionality to occur, we need to make sure that these two rules are fulfilled:
- As A gets bigger, B gets smaller.
- What increases one decreases the other. This is, for example, if A is doubled then B is halved. Or if B triples then A is reduced by a third.
This means that the proportion between the two magnitudes is inverse.
For example, in the following table, you can see A and B’s magnitudes:
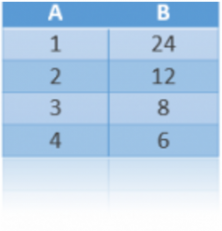
It’s an inverse proportionality because as long as A gets bigger, B gets smaller which is exactly what Rule 1 outlines.
Additionally, when A is doubled, B is halved (in the second row on the table we can see that A is worth 2 and B, 12). When A triples (going from 1 to 3), B’s value drops from 24 to 8, which is one-third of 24. Looking at the final row, if A is worth 4, B is reduced to 6 which is one-quarter of what it was worth when A was 1. As a result, Rule 2 has been fulfilled.
How Do We Use the Rule of Three Inverse?
The rule of three inverse is used in problems where three of the four numbers that are proportional are known and the fourth number is what needs to be solved.
First, we need to relate A to B. Then, we write down the next pair of numbers that we need to relate.
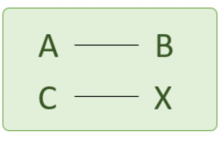
C is magnitude A’s value and X, the value we are solving for, is magnitude B’s value.
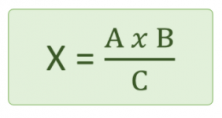
How Do We Solve a Problem with the Rule of Three Inverse?

At a farm, it takes 10 days for 20 ducks to eat the food that’s left out for them. How much time would it take for 40 ducks to eat the same food?
First, we have to determine if the proportionality is direct or inverse:
It takes 10 days for 20 ducks. 40 ducks…would it take them more or less time to eat the food?
If the number of ducks increases, then the number of days the food will last decreases and it is possible to think that if there are twice as many ducks then they will eat the food in half the time. So it is inverse proportionality.
Now, let’s apply the rule of 3 inverse:

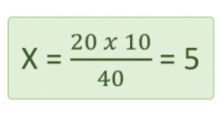
It will take 5 days for 40 ducks to eat all the food.

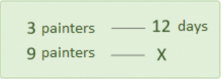
It takes 12 days for 3 painters to paint a house. How long will it take for 9 painters to do the same job?
First, we need to determine which kind of proportionality it is.
It takes 12 days for 3 painters. 9 painters…will they take more or less time to do the job?
Since there are more painters it will take less time to finish the work and it is reasonable to think that with three times the amount of painters that the job will be done in a third of the time. Therefore, it is inverse proportionality.
Now, we just need to apply the rule of three inverse:
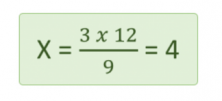 It takes 4 days for 9 painters to paint the house.
It takes 4 days for 9 painters to paint the house.
If you would like to keep learning and practicing elementary math adapted to your level, register with Smartick and try it for free.
Learn More:
- Inverse Proportionality: What Is It?
- Compound Rule of 3: When to Use It and Some Problems
- Direct Proportions: What Are They? What Are They Used For?
- Direct and Inverse Rule of 3 Problems
- Proportionality Problems: Learn How to Solve Them








well explained
Good examples.😊😊