Rekenrek Vs. Soroban
At Smartick, we use the abacus as a visual model to learn how to calculate. Some other well-known methods, like Aloha or UCMAS, use the traditional Japanese abacus, the Soroban, as a means to reach the same goal.
We’ve opted for a different kind of abacus: the Rekenrek. The Rekenrek is an abacus designed by the Dutch professor Adrian Treffers in 1991. In this entry, we’ll explain why we prefer the Rekenrek, focusing on the relationship between the abacus and the hand.
In the picture below, we can see the relationship that’s established between counting with fingers and counting with the abacus. First of all, children learn how to use their fingers to represent quantities. Then, they use an analogical instrument with the same structure, like the Soroban.
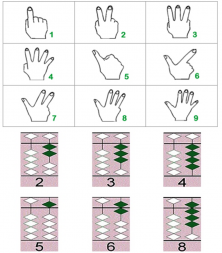
Upon examining this system, we want to highlight an important aspect from the teaching point of view. The method of using fingers in “finger counting” that we see in Aloha doesn’t coincide with the natural way in which elementary students learn how to represent quantities with their hands.
Number 5
The number 5 is shown with the thumb, just like we see in the Soroban. Since the thumb has a value of five, the number seven is represented by the thumb, pointer finger, and middle finger…three fingers! Children that learn how to use the Soroban learn how to show quantities with their fingers first. Next, they learn this new and sophisticated way of showing quantities with fingers, where the thumb has a value of five, and the fingers represent one. Finally, they use what they learned to use the Soroban.
At Smartick, we also form a relationship between how hands are used to represent quantity and the Rekenrek. However, the Rekenrek leans towards learning based on the way children naturally use their hands to express quantities. Children show the number seven with seven fingers, using one whole hand and two fingers from the other, as shown in the picture below:
This is the way children commonly learn. They begin using one finger to show their age at their first birthday and continue learning to use their fingers to show quantities right up until the end of elementary school. By choosing the Rekenrek method, we are taking advantage of this natural learning flow to form relationships between the hand and the Rekenrek. This transfers all of that learning to the Rekenrek, creating a meaningful learning experience.
The number five is very important to both the Rekenrek and the Soroban and is recognized as a helping unit for calculations. This is because, as we’ve seen, both of them “copy” hand structure.
However, we see an important duality in hands: the hand has five fingers yet it can also be seen as one (the hand) or 5 units (the five fingers). It’s both one and five. The Rekenrek reflects this; a group of five red counters represents the hand (the entire group of red counters) and the five fingers (each individual counter).
When using the Soroban, the superior counter represents 5, (the thumb), but five components are never represented by that counter. The thumb does not represent five individual components either; rather, the representation is a result of a convention.
This difference is extremely important from a teaching point of view. When children start elementary school, they’re confronted with a composed unit. It’s one whole thing (one group of ten) and, at the same time, something that’s composed of ten individual units. Therefore, it’s convenient for children to visualize this double meaning, as they do when they see a bar of ten made with Dienes blocks; it’s both one whole (a bar of ten) and ten parts (cubes or units).
To summarize, we believe that the Rekenrek is based on the natural way of learning numbers, while the Soroban uses elements that are difficult for a young child to understand.
Learn More:
- Rekenrek Vs. Soroban II: Varied Strategies for the Same Calculation
- The Importance of Finger Counting
- Learn to Add Using the Rekenrek
- Do You Want to Learn Multiplication Tables Tricks?
- Tens and the Decimal Number System
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.