Oct31

How to Solve a 1 Digit Division Problem

Hello! Today we’re going to learn how to solve 1 digit division problems. Are you ready to end October with a 1 digit division problem?

First, we need to know the parts of a division problem:

Dividend: The number that you have to divide.
Divisor: The number that the dividend is being divided by.
Quotient: The result of the division.
Remainder: What is left over after the division.

Look at how we set up each part of the division:

1 digit division

Now, let’s see how a 1 digit division problem would look if we replace each word with a number:

We want to divide 243 pieces of candy among 5 friends.

The dividend will be 243 because it’s the number that we want to divide.

The divisor is 5 because it’s the number that we are going to divide the 243 pieces of candy by. 

The quotient will be the number of candies that each kid will get.

The remainder will be the number of candies that are leftover.

So then, how do we solve for the quotient and the remainder of a 1 digit division problem?

We start with the first number of the dividend, dividing it by the divisor. If this number is smaller than the divisor, we’ll need to use another number of the dividend. In our example, the first number of the dividend is 2, but since it’s smaller than the divisor, which is 5, we have to use another number: 24. Now, we can begin dividing 24/5.

The next step of our division problem is to find a number that we can multiply the divisor by that gives us the same number as the dividend. If one doesn’t exist, we’ll have to find the closest possible number that’s still smaller than the dividend. The answer we get from multiplying is subtracted from the dividend. Following our example: we have to divide 24 by 5. So, we need to look for a number that gives us 24 when multiplied by 5. Since an exact number doesn’t exist, we have to use the closest smaller number: 4 x 5 = 20. In this case, 20 is the closest number to 24 that doesn’t surpass it. So, we write 4 in the quotient and subtract 20 from 24, and we have 24 – 20 = 4

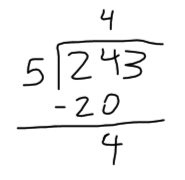
1 digit division

There’s only one more step for us to do in order to complete the 1 digit division problem: bring down the next number of the dividend and repeat step 2.

We bring down the next number, which is the number 3, and write it next to the number 4. The complete number is 43.

Now, we divide 43 by 5. We have to find a number that gives us 43 when multiplied by 5. But, since it doesn’t exist, we have to find the closest number that doesn’t surpass 43. In this case, it’s 5 x 8 = 40. So, let’s write the 5 in the quotient and the 40 underneath the 43 to subtract it: 43 – 40 = 3.

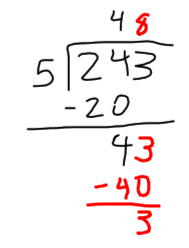
1 digit division

There are no more numbers in the dividend, so we are done with the division problem.

The answer to our 1 digit division problem is: every kid will get 48 pieces of candy and 3 pieces of candy will be leftover.

That’s all from me until next Wednesday. I hope you learned how to solve 1 digit division problems.

Have a great week!

And if you want to learn more math, try Smartick for free!

Learn More:

Fun is our brain’s favorite way of learning

Diane Ackerman

Smartick is a fun way to learn math

15 fun minutes a day
Adapts to your child’s level
Millions of students since 2009

Author
Recent Posts

Smartick

Content Creation Team.
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.