In today’s post, you will learn the difference between prime and composite numbers. Additionally, we will show you several examples to help you understand them better.
Index
What Are Prime Numbers?
Prime numbers are the numbers that are only divisible by themselves and 1, in other words, if we try to divide them by another number, the result is not a whole number. So, if you divide the number by anything other than one or itself, you will get a remainder that is not zero.
Prime Numbers Until 100
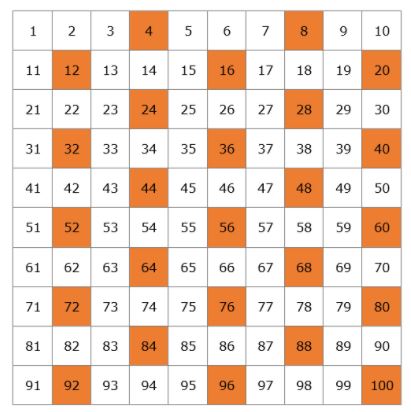
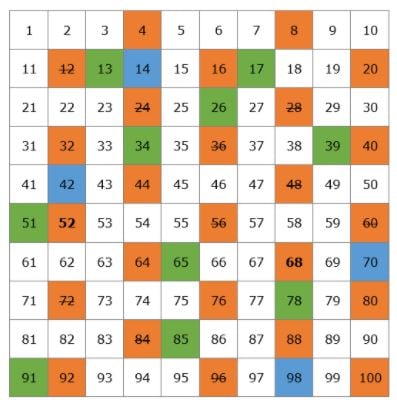
We are going to create a table with all of the prime numbers that exist up to 100.
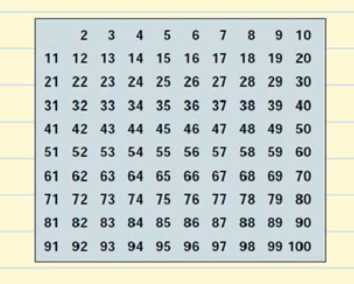
Let’s start with 2. 2 is a prime number but all of the multiples of 2 will be composite numbers since they will be divisible by 2. We cross out all of the multiples of 2 on the table.
The next prime number is 3, so we can cross out all the multiples of 3 since they will be composite numbers.
After 3, is the next prime number 5, so we cross out all of the multiples of 5.
Then we have the prime number 7 and we cross out all of the multiples of 7.
The next prime number is 11, so we cross out all of the multiples of 11 which are 22, 33, 44, 55, 66, 77, 88, and 99. All of these numbers had already been crossed out so we have finished crossing out all of the composite numbers on our table.
This is our list of prime numbers from 1 to 100. You don’t have to memorize them but it would be best if you remember the smaller numbers, such as 2, 3, 5, 7, 11, 13.
How Many Prime Numbers Are There?
The Greek mathematician Eratosthenes (3rd-century B.C) designed a quick way to find all the prime numbers up to any given number. It’s a process called the Sieve of Eratosthenes.
Notice that between 1 and 100 there are 25 prime numbers. How many prime numbers are there in total? We have known since ancient times that there are an infinite amount, so it is impossible to list all of them. Since Euclid, who was the first to show that there were an infinite amount in 4th century B.C, did not know the concept of infinity he said ”prime numbers are more than any fixed multitude of them” meaning if you imagine 100, there are more, and if you imagine one million there are still more.
Prime Numbers 100 to 1,000
Let’s take a look at the prime numbers from 100 to 1,000.
We’re sorry that we can’t show all of them, as you know there is an infinite amount. 😉
Prime Numbers Examples
To help you better understand prime numbers, we are going to explain an exercise.
Sara has 6 pieces of candy that she wants to share, but she doesn’t know how many people she can share them with so that everyone gets the same amount and none are leftover. How many ways can she do this?
Here is Sara and her 6 pieces of candy:
How can we divide them?
The first and easiest way is to give them to one person, in other words, divide by 1. This way that person will have 6 pieces of candy.
The next possibility is to divide them between 2 people. Since 6 divided by 2 is 3, each person gets 3 pieces of candy!
We are going to continue with the next number, 3. If we divide 6 pieces of candy between 3 people it is also an exact division and each person will get 2 pieces of candy:
Let’s continue with the numbers. We do not have exact divisions with 4 and 5, but we do with 6.
Since 6 divided by 6 is 1, we can give 6 children 1 piece of candy each.
We’re going to collect some information. We have 6 pieces of candy that we can share (with an exact division) between 1, 2, 3, and 6 people. In other words, we can divide the number 6 and get 0 as a remainder when we divide it by 1, 2, 3, and 6. These numbers are known as the divisors of 6.
We are going to try with another number, 7 for example.
Now Sara has 7 pieces of candy and wants to share them, but doesn’t know how many people she can share them with so that everyone gets the same amount and none are leftover. How many ways can she do this?
Henry is so lucky! He got all of the pieces of candy!
Are there other ways to do it? We cannot divide 7 by 2, 3, 4, 5, or 6, …but 7 is possible!
Sara can share the pieces of candy between 7 people, giving them one piece each:
So 7 can only be divided by 1 and 7, its only divisors are 1 and 7. These are the types of numbers we call prime numbers.
Are there more prime numbers? Of course! Let’s look for some more:
- Is 4? No! Because its divisors are 1, 2, and 4.
- Is 5? Yes! Because its divisors are 1 and 5.
- Is 8? No! Because its divisors are 1, 2, 4, and 8.
In short, a number is prime if it only has 2 divisors: 1 and itself.
Now you can search for lots of prime numbers!
How to Find Prime Numbers
Pay close attention! We are going to give you a trick to know if a number is prime or not, without having to look for its divisors, but in a way that is more fun and gives us the divisors (if they have them).
Let’s pick a number at random, 16 for example.
To check if it is a prime number or not, we are going to use a table that is very similar to Montessori cards to multiply. And we will get as many balls as the number we have chosen. In this case, 16 balls.
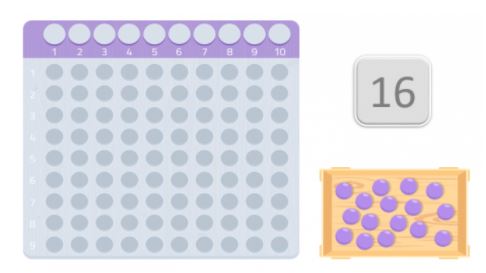
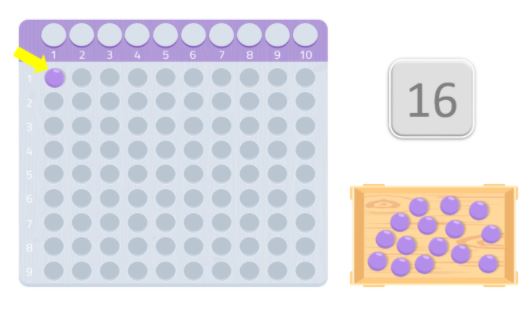
Once we have the table and the balls, we should place them on the table beginning with the first space, trying to form a rectangle. The numbers that make up the edges of the rectangle are that number’s divisors.
In case we only manage to form a rectangle with the same number that we are using and the number 1, it will be a prime number.
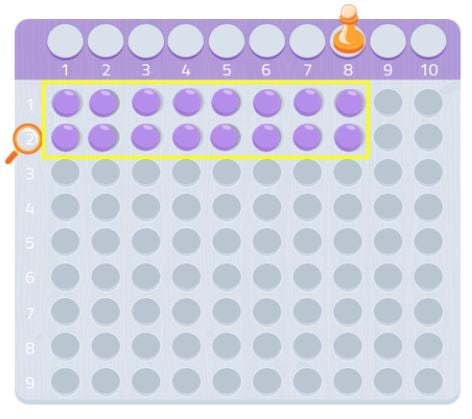
For example, in this case, we place 8 balls in the first row and 8 more in the second. As you can see, we have formed a rectangle and we can see that 8, like 2, are divisors of the number 16. Therefore, 16 is not a prime number because, as you know, prime numbers are those that are only divisible by themselves and 1.
We can try with another number, 7 for example.
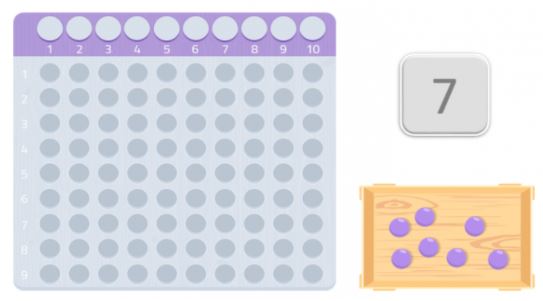
As we can see, we couldn’t make a full rectangle, we would be missing a ball. Since we are unable to form a rectangle, we could say that the number 7 does not have any other divisors except for itself and 1, as we can see in the following image.
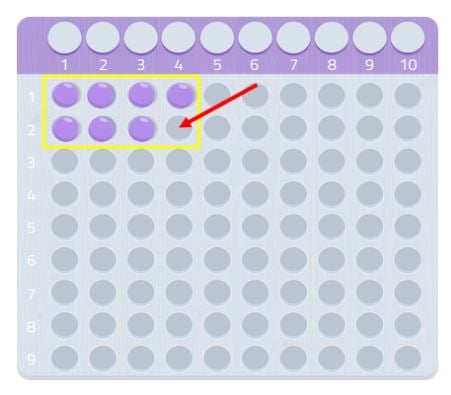
Therefore, 7 is a prime number!
Try any other number, you’ll see how it works! You can use graphing paper and look for rectangles using that number of squares.
Why Are Prime Numbers Important?
Prime numbers are the key to arithmetic, below you will see an example that demonstrates their importance, not just in mathematics but also in nature.
What do we mean when we say that prime numbers are the key to arithmetic?
This is because any number consists of a unique product made up of a series of these numbers.
It is believed that they have been studied for about 20,000 years when an ancestor of ours wrote down a series of prime numbers (11, 13, 17, and 19) on the Ishango bone. As if this were a coincidence, it has been confirmed that the ancient Egyptians were working with them 4,000 years ago.
In addition, nature knows them very well and some species have been able to discover them throughout their evolution and take advantage of them for survival.
I am referring to several species of cicadas, such as the Magicicada septendecium that lives in North America. This species of cicada has established its breeding cycle around 13 or 17 years, not 12, 14, 15, 16, or 18 – exactly 13 or 17. This allows them to avoid predators that also have periodic reproductive cycles; imagine a predator with a 4-year reproductive cycle.
If the life cycle of a cicada were 12 or 14 years, it would coincide with a predator very frequently, much more than if it were 13 or 17 years. Exactly 2 times every 100 years, while otherwise, they would coincide in 11 cycles which would compromise the development of the species.
The security of electronic communication is based on prime numbers as well. Every encrypted message sent over the internet (message networks, purchases, or electronic banking) has a large number associated with it, and it is very difficult to know where it is prime or not. The receiver has one of its divisors, and that’s why they can decrypt it. So having prime numbers is critical to our privacy when communicating electronically.
What Are Composite Numbers?
Composite numbers are those numbers that are divisible by 1 and themselves as well as other numbers.
We are going to look at an example of a prime number and a composite number.
11 can be written as the multiplication 1 x 11, but it cannot be written as any other multiplication of natural numbers. It only has the divisors 1 and 11, and therefore it is a prime number.
12 can be written as the multiplication 1 x 12 and as the multiplication 3 x 4, and 2 x 6. Since 12 is divisible by more numbers than 1 and itself, 12 is a composite number.
Is 1 a Prime Number?
There are people that believe so because they say that 1 can only be divided by 1 and itself but in mathematics, the number 1 has been discarded as a prime number because it only has one divisor. In fact, the criteria of ”a positive integer is prime if it has exactly two positive divisors” is used to exclude the number one from the prime number list. It is not because we are being picky about it, but if the number one was considered prime then many mathematical properties would have to be said differently.
So, 1 is a Composite Number?
Well, it is not composite either since it cannot be put as the product of prime numbers. The number 1 is not prime or composite. And before you ask, zero is not prime or composite either but this is because all of the considerations we were explaining for positive numbers, that is, greater than zero.
Divisors of a Number
The divisor of a number is the value that divides the number into exact parts, in other words, has a remainder of 0.
As an example, we are going to calculate the divisors for 24.
We begin dividing with the smallest numbers starting with 1.
- 24 / 1 = 24. Both 1and 24 are divisors.
- 24 / 2 = 12. So 2 and 12 are divisors.
- 24 / 3 = 8. So 3 and 8 are divisors.
- 24 / 4 = 6. So 4 and 6 are divisors.
- 24 / 5 = 4. It is not an exact division and has a remainder of 4 so 5 is not a divisor.
The next number is 6, but since we already know that 6 is a divisor of 24 we have finished calculating the divisors for 24.
Video: Factorization and Prime Numbers
If you would like to know more about prime and composite numbers, take a look at the following video. You will also learn the concept of factoring by using the Montessori table.
This video is one of our interactive tutorials and, although it is not interactive, you can still watch it as many times as you need to and share it with friends. If you would like to access our interactive tutorials, register with Smartick! The online method to help children ages 4 to 14 learn and practice mathematics.
If you would like to continue learning about prime numbers and the best mathematics adapted to your level, register with Smartick and try it for free!
Learn More:
- Learn How to Factor into Prime Numbers
- Prime Numbers Activities with Smartick
- Some Prime Number Curiosities
- What Is a Number? Learn to Count up to 9
- Divisibility Criteria from 2 to 13 and an Example
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.
l like mathematics because it’s my area of study and love it for a better living.
nice
But how can I become a prime member
🤣🤣