We are going to dedicate this entry to working with manipulative materials known as algebra tiles. Although you may have a good idea of this topic, it is always good to go back and refresh your memory – we recommend this post.
Are you ready? Well, let’s go!
How to Subtract Polynomials
Our goal is going to be to solve this subtraction problem with polynomials by using this material. In order to do so, we must incorporate some new elements into the model that were presented for addition. In particular, these new elements will consist of using different color algebra tiles.
- green for the positive terms
- red for the negative terms
So, to subtract two polynomials using this tool, the first thing we need to do is represent them adequately. For example, if we want to solve:
(2x2 – 3x + 3) – (x2 – x – 1)
We need to first correctly represent the polynomials involved. Let’s do it!
The polynomial (2x2 – 3x + 3) is composed of 2 positive x2 tiles, 3 negative x tiles and 3 positive unit tiles:

For the other side, the polynomial (x2 – x – 1) is formed by 1 positive x2 tile, 1 negative x tile and 1 negative unit tile:

Now it’s time for the step that we need to be the most careful with. We have to remember that subtracting a polynomial is the same as adding the result that comes from changing the signs of all its terms. This way, we change the color of the algebra tiles that form the result of the polynomials we have subtracted:

We group the like terms and cancel out a green tile for each red tile:
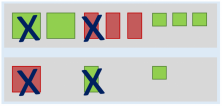
We’re almost done! We analyze the result of the subtraction problem we have solved. In our example, there was 1 positive x2 tile, 2 negative x tiles, and 4 positive unit tiles:

Finally, we write the polynomial we have obtained and we have the solution to our subtraction problem:
(2x2 – 3x + 3) – (x2 – x – 1) = (x2 – 2x + 4)
Have you seen how easy it is to use algebra tiles to solve math problems with polynomials? Well if you want to keep practicing this and other math contents, sign up with Smartick and try it for free.
Learn More:
- Representing Polynomials with Algebra Tiles
- Review the Properties of Polynomials
- Learn How to Add Polynomials with Examples
- Learn to Subtract with Remainders
- How to Solve a Subtraction Problem with Regrouping







