In this post, we are going to explain the properties of powers. We will also try to justify the reasoning for following them. Before we begin, let’s remind ourselves of what a power is.
What Is a Power?
A power is the product of a number multiplied by itself a certain number of times. In other words, a power is the product of equal factors. This idea can be written like this:
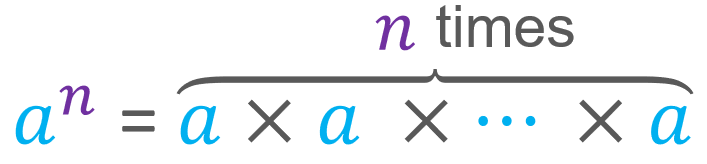
The repeated factor, a, is known as the base, while the number of times it is repeated, n, is the exponent.
You can find more information about powers in this post. Once you have refreshed your memory about what a power is, we can continue with their properties. However, let’s first establish that the base has to be different from 0. After all, who is interested in multiplying by zero? 😀
The Properties of Powers
Multiplication of Powers with the Same Base (Product of Powers)
Sometimes we come across products of powers with the same base. For example:
23 × 25
62 × 67
In such cases, we may be interested in using this property. Look closely at the following equation. Take note that it can be solved because it fulfills the associative property of multiplication and the order of the products does not make a difference.
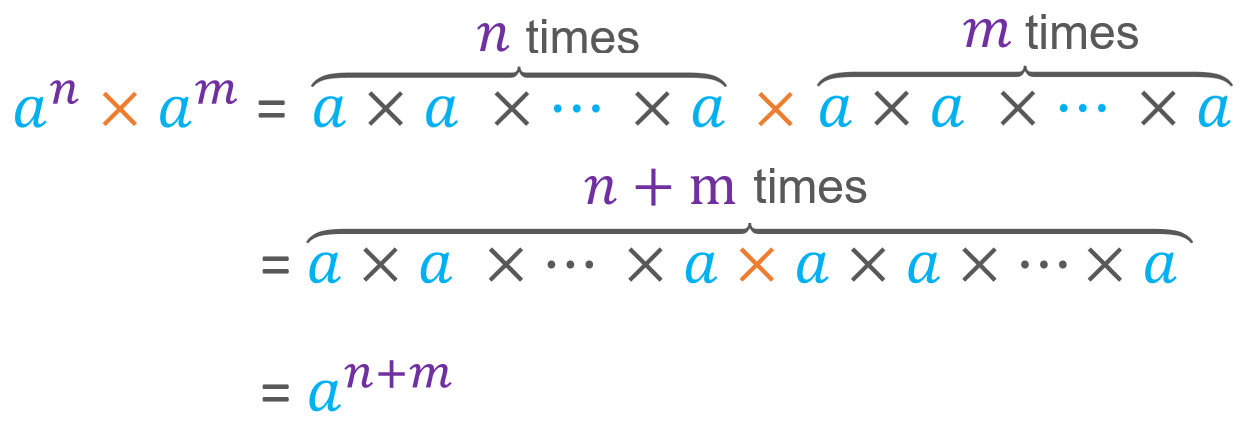
This property can be read as multiplying powers with the same base is equal to keeping the same base and adding the exponents.
Keep in mind that the equation can also be read from right to left. Namely, you can group the factors of a power however you want in order to find the product of two others with smaller exponents. For example:
210 = 27 × 23
Division of Powers with the Same Base (Quotient of Powers)
Something similar to what we have seen with multiplication also occurs with division. Remember that in a fraction, repeated factors in the numerator and denominator can be simplified. Take a look at this!
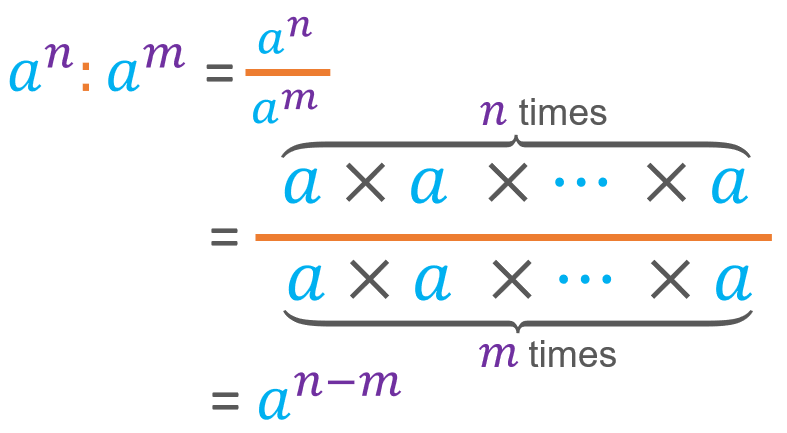
This property states: dividing powers with the same base is equal to keeping the same base and subtracting the exponents. As with the previous example, it can be read and completed in the opposite direction. For example:
53 = 57 − 4 = 57 : 54
Powers with Zero Exponent
If we look at the property above we can understand a power with a zero exponent as a ratio between equal powers. For example: 23 : 23, as well as, 52 : 52, and 34657 : 34657
In general, this applies to any nonzero base with any exponent. Furthermore, what is a fraction with the same numerator and denominator equal to? Well 1, of course.
Therefore, any number raised to 0 is 1.
Powers with a Negative Exponent
Something similar also occurs in powers with negative exponents. If you look at the property of dividing powers with the same base, if m is greater than n, then subtracting n – m results in a negative number. Therefore, it is not uncommon for a power with a negative exponent to be a fraction with factors only in the denominator.
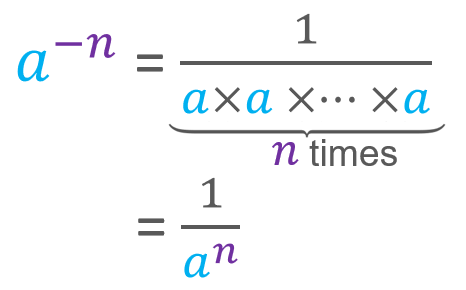
In other words, that a power with a negative exponent is equal to a unit fraction that has a denominator with the same power, but with a positive exponent.
I hope that this post has helped you to understand the main properties of powers. If you would like to keep practicing similar exercises like this, and many more, join the Smartick community.
Learn More:
- Properties of Powers II
- Do You Want to Learn the Properties of Powers?
- Learn More about Exponents
- Powers in Math
- Learn about the Importance of the Parentheses in Powers







