In this post, we are going to learn all about Cartesian coordinates: what they are, what they are used for, and how they work. Additionally, you will see some examples of coordinate exercises that children do during their personalized, daily Smartick sessions.
Index
What are Cartesian Coordinates?
When we play Battleship we say a letter for the vertical position and a number for the horizontal position when we try to locate our rival’s boat. When we play Battleship we are using Cartesian coordinates.
Cartesian coordinates is the name given to the system used to locate a point in space. We work on Cartesian coordinates in a two-dimensional space, on a plane, but we can also use them in spaces of three or more dimensions. The “last name” of the cartesian coordinates is a tribute to the philosopher and mathematician René Descartes.
A Cartesian coordinate system is formed by two straight perpendicular lines, which we call coordinate axes. The horizontal axis is usually named X and the vertical axis is Y. These two axes cross at a point called the coordinate origin, O.
Another name given to the axes of coordinates are abscissa for the X-axis (horizontal) and ordinate for the Y-axis (vertical).
When we want to know what the points of a certain coordinate are (which we usually name with capital letters like P, Q, R or A, B, C) we just keep in mind that they are placed like this:
(abscissa, ordinate)
So if we say that point P has coordinates (3, 5) we are saying that it is located at point 3 on the horizontal axis and point 5 on the vertical axis.
How do Cartesian Coordinates Work?
If we want to indicate something on a plane, we need:
- A horizontal measurement: left-right. We call this X.

- A vertical measurement: up-down. We call this Y.

- A reference point from which we can measure: the origin. We call this O.
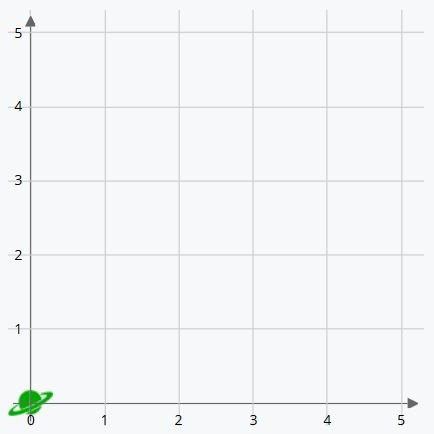
O, the origin, is where you can see the green planet in the image above. It’s called the origin because it’s the point from which the lines that delineate the two axes of the coordinates originate.
Let’s look at the horizontal line, left-right. As you can see, the numbers start at the origin. The first value is zero and the numbers increase as we move to the right. This is the X-axis of the coordinates, and the larger its value, the farther to the right the dot is placed. So, 4 on the X-axis is 4 positions to the right of the origin.
We also have a vertical line, up-down. In the same way as the X-axis, the values start at the origin with zero and increase as we move upwards. This is the Y-axis of the coordinates. The larger its value, the higher we go. For example, 5 is five positions above the origin.
In the game “pin the tail on the donkey” we need the other players to tell us how far to the left or the right and how far up or down we need to move to pin the tail correctly. To indicate a point on a plane we need to do the exact same thing. We need to plot two numbers: one on the X-axis and the other on the Y-axis. This defines the position: the first number indicates how far to the right it is and the second number how far up it is. These numbers are usually separated by a comma and placed inside parentheses, like this: (X , Y).
Examples of Coordinates
The origin is always situated at the coordinates (0,0). In other words, it’s the lowest point possible, and farthest to the left. O is a special point from which the axes of the coordinates originate and is “0 positions to the right and 0 positions up.” This is the point from which we start to count. Therefore, (0,3) will be 0 positions to the right and 3 up. And (5,0) will be 5 positions to the right and 0 up.
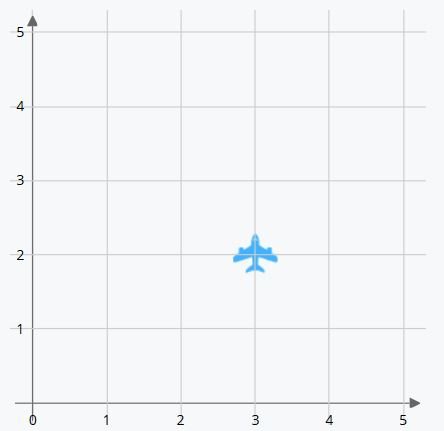
For example, a blue airplane is at the coordinates (3,2) Where will we find it?
The first coordinate we’re given is the position on the X-axis. We have to count 3 positions to the right from the origin. The second coordinate gives us the position on the Y-axis, so we count 2 positions up. Therefore, we place the blue plane 3 positions to the right of the origin and 2 places above.
Now let’s look at an inverse example. We place the object first and then indicate the coordinates of the position it’s in: What coordinates is the orange tree at?
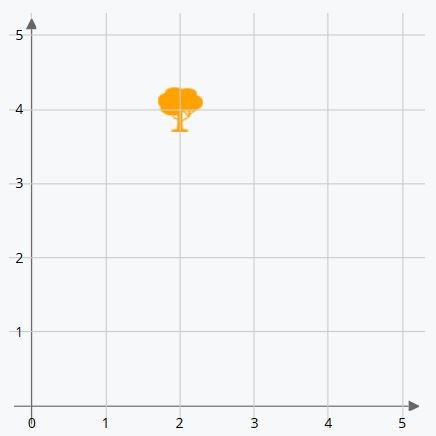
We can see that it’s situated two positions to the right of the origin (X-axis) and 4 above (Y-axis). First, we write the X-axis coordinate and then the Y-axis coordinate.
The orange tree is at the coordinates (2,4).
What are Coordinates Used For?
Aside from their use in mathematics, we can find coordinates used on a daily basis to indicate places on maps. Maps can be divided into sectors with horizontal and vertical axes. The map can show a few streets, a city, or the entire world. So you can find your friend’s house with a map of their city or even where an attraction is in your favorite amusement park.
Another context where we frequently find planes and coordinates is when we use a GPS. But remember, even if we see a plane on the screen, a GPS does not give Cartesian coordinates because the Earth is a sphere and the GPS uses geolocation using satellites. The values used by a GPS are those of latitude (how far we are north or south of the Equator) and longitude (how far we are east or west of the Prime Meridian). You can check out this post about what an angle is and how to measure them.
Quadrants
So far we have only considered the part of the plane in which both the X-axis, abscissa (horizontal), and the Y-axis, ordinate (vertical) are positive numbers, but they can also be negative. If you need to, you can take a look at our post about how to place numbers on a number line, because when we use Cartesian coordinates what we are really using are two number lines that cross each other perpendicularly. This means that coordinates can also contain decimals, although in this entry we will only be using whole numbers so as to not complicate things
As we mentioned, the Cartesian coordinates are used in two dimensions (plane). The axes (X and Y) cross perpendicularly at the origin (O), dividing the plane into four regions:
These regions are called quadrants and are numbered from 1º to 4º with Roman numerals. They are numbered counterclockwise using the origin as the central point.
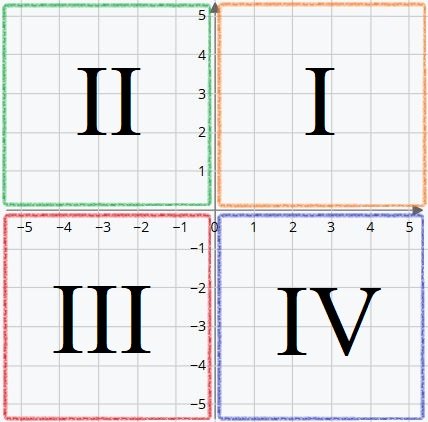
First Quadrant
Until now, we only knew the origin ‘O‘ and the first quadrant. In it, the coordinates X and Y are always positive numbers.
- X positive means that the position is to the right of the origin.
- Y positive means that it is above the origin.
So, in this quadrant, (X, Y) are positive. We can write them abbreviated as (+,+).
The yellow dot is at the coordinates (3,3). Three positions to the right of the origin and three above.
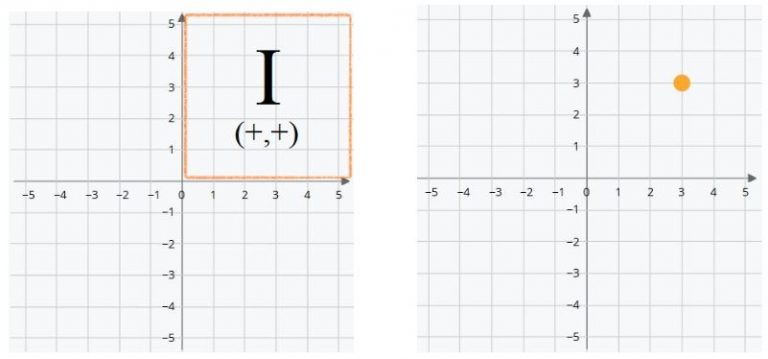
Second Quadrant
The first negative coordinate appears in this quadrant. The positive values tell us how many positions to count to the right or above the origin, X and Y respectively. In the same way, the negative values indicate how many positions we count to the left or below the origin of the X and Y axes. For example, if the X coordinate has a value of (-5) it means that it is 5 positions to the left of the origin. If the Y coordinate has the value of (-1), it means that it is one position below the origin.
- X negative indicates that the position is to the left of the origin.
- Y positive that it is above the origin.
Thus (X,Y) are written (-,+).
In the example, the green dot is at the coordinates (-3,1). Three positions to the left of the origin and one position above.
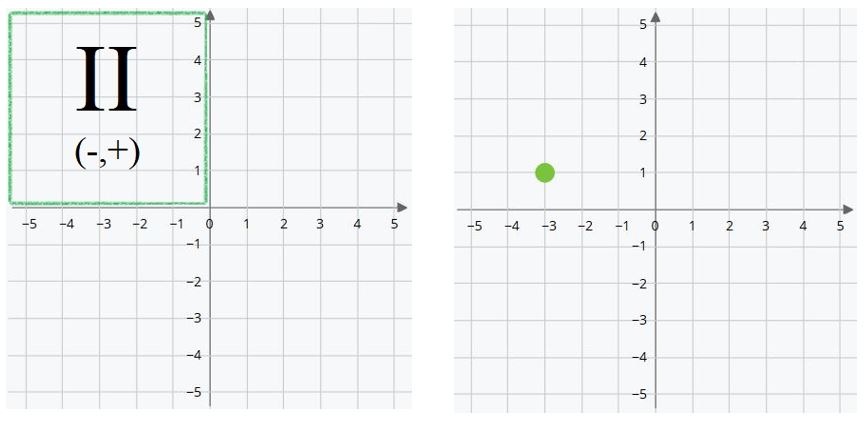
Third Quadrant
Here, both values are negative.
- X negative indicates that the position is to the left of the origin.
- Y negative that it is below the origin.
Therefore (X, Y) are written (-,-).
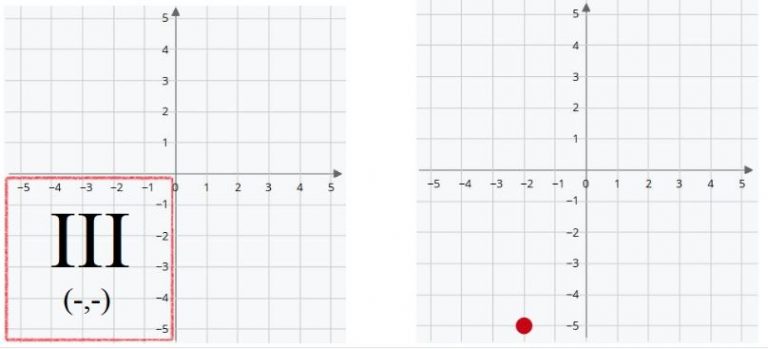
The red point is on the coordinates (-2,-5). Two positions to the left of the origin and five positions below.
Fourth Quadrant
The last quadrant is to the right and below the origin. The values of X and Y will be positive and negative respectively.
- X positive indicates that the position is to the right of the origin.
- Y negative that it is below the origin.
In other words (X, Y) are written (+,-).
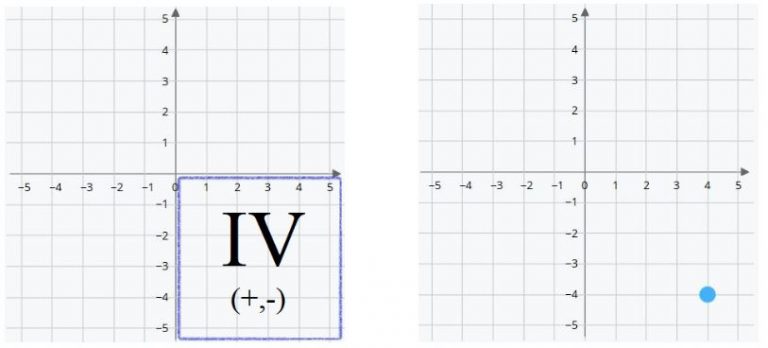
The blue dot is at the coordinates (4,-4). Four positions to the right of the origin and four below.
To summarize, the positive or negative value of the X and Y coordinates indicate their relative position with respect to the origin:
- On the X-axis, horizontal direction, a positive value reflects a position to the right of the origin. And a negative, to the left.
- On the Y-axis, vertical direction, the positive value indicates a position above the origin while a negative value indicates one below.
- If X has a value of zero, the position of the coordinate is not to the right or left of the origin. It would be at some point on the Y-axis.
- If Y has a value of zero, the position of the coordinate is not above or below the origin. It would be at some point on the X-axis.
- O, the origin, is the only position in which both values are zero.
In conclusion, knowing the values of (X, Y) we can know which quadrant that position is in according to the following framework:
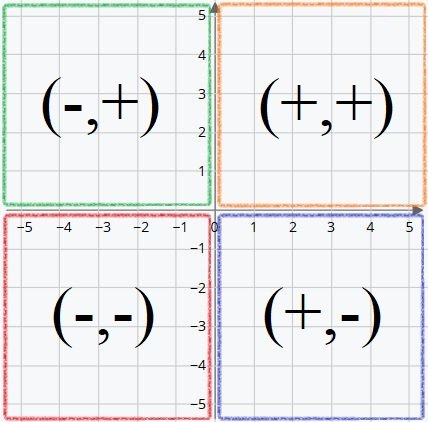
Examples of Coordinate Exercises in Smartick
The placement of Cartesian coordinates has three elements:
- The initial position: the coordinate in which it starts.
- The movement: the movements carried out.
- The final position: the final coordinate after the movement.
Known Initial Coordinates and Simple Movement with Visual Help in the First Quadrant
In these exercises, the initial position and movements are given, and they only contain one movement. We only use the first quadrant and ask for the final position after seeing the movement. In addition, we offer a visual aid for the first few tries. The axes are different colors and the coordinates assigned to these axes maintain the same color code. Since these exercises are being solved by young children, instead of placing the numbers on the line (and the characters at their intersections) we place them in the center of the space so that it is easier to see, but the result is the same.

In this example, Zoe begins at the coordinates (2,1) and moves one space to the right. Since she only moves along the X-axis, only the X coordinate changes. Her final position will be (3,1).
Known Final Coordinates with Several Movements in the First Quadrant
It is the same as the previous example with one difference: the number of movements is increasing.
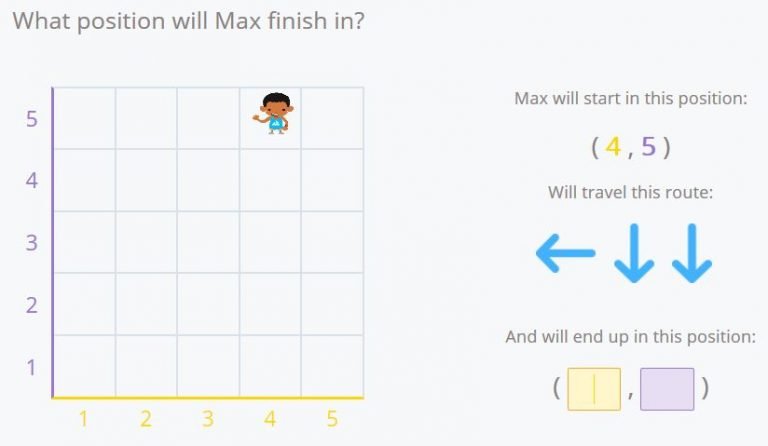
Max had started at the coordinates (4,5). He’s moved once to the left and down two times. If we follow his movement along the grid we see that the final position is (3,3).
Known Final Coordinates with Visual Help in the First Quadrant
Now, in place of the final position, we’re looking for the starting position. Knowing where they finish and the movements they have made, we can calculate their path in reverse.

Here, Amy has moved once to the right and has finished at the coordinates (4,4). Following her movements in reverse (one space to the left) we can verify that the origin position was (3,4).
The difficulty will increase as the number of movements increases.
Numerical Help in the First Quadrant
We also ask for the final or starting position, but no longer offer help by using colors to identify each one. Additionally, the coordinates become points on the plane instead of squares. If you look closely instead of Eva being in the center of the space, she is already at the intersection of two lines.

Here Eva begins at the position, (4,3). She moves once to the right and down two times. If we follow her movements we can see Eva’s final position is (5,1).
All the Quadrants
The dynamic is the same as the previous activities but the rest of the quadrants have been added.
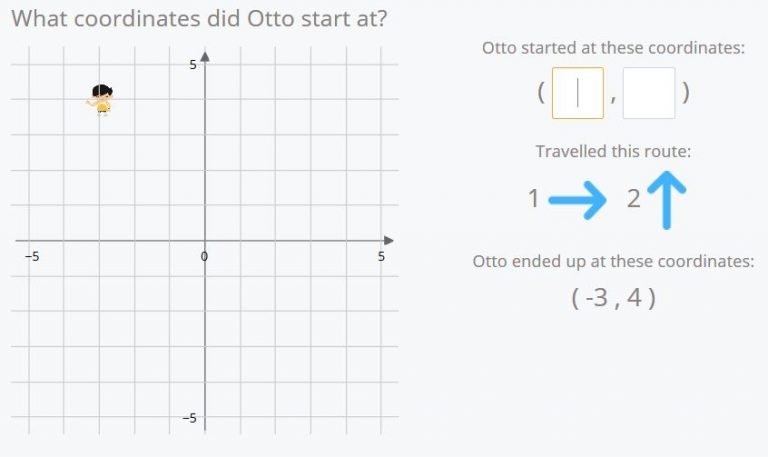
Otto has moved once to the right and up two times. He’s ended at the point (-3,4). If we follow his path in reverse (once to the left and down two times) we see that his origin coordinates are (-4,2).
And finally, we made the grid where you can move the avatar bigger.
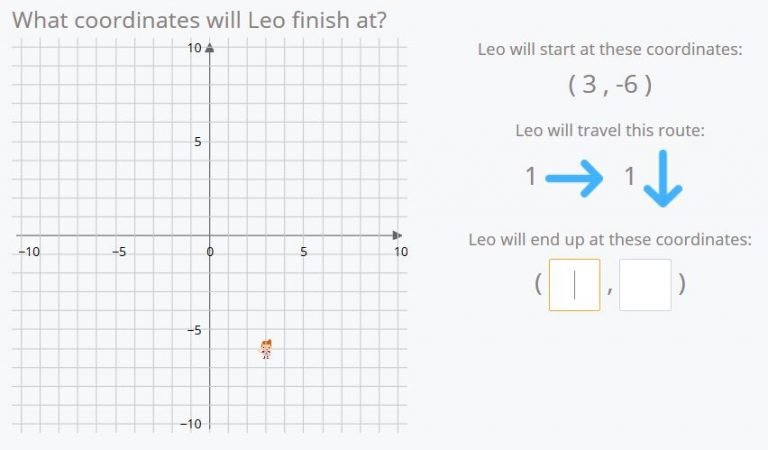
If Leo begins at the position (3,-6) and he moves once to the right and down once…..where will he end?
That’s it! He will end at (4,-7).
If you would like more practice, or to learn more about coordinates and other elementary math topics adapted to your level register with Smartick and try it for free.
Learn More:
- Mathematical Functions: Do You Know What They Are?
- Symmetry: What It Is And How to Find It
- The Language of Functions and Graphs
- Identifying Flat Symmetrical Figures
- Multiplying and Dividing Decimal Numbers by Powers of 10







