As we said in a previous post, we are going to analyze different chapters from Craig Barton’s book, How I Wish I’d Taught Maths, about evidence-based education.
Today we will speak about the first chapter which focuses on how students think and learn.
A simple model for thinking and learning
Barton considers it important to establish a simple model that represents how students think and learn.
It points to two different areas involved in thinking:
- Long-term memory is where information is stored until it is needed. It has unlimited capacity. Schemes and relationships are established. Together this information is what is known as knowledge.
- Working memory is where thought occurs, recovers information from long term memory and becomes conscious. It has a limited capacity.
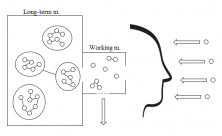
The key to reasoning rests on a few factors:
- Exterior information.
- Facts and procedures stored in long-term memory.
- The capacity of working memory.
If any of these are deficient, it is likely that the reasoning is not successful and learning does not happen.
It also establishes learning as changes in long-term memory and working memory as the tool to produce these changes. It’s a two-way street. Students learn new concepts in reference to ideas they already have. They keep this information in working memory to establish relationships and then go back to long-term memory. On the other hand, as long-term memory information is retrieved for use in working memory, long-term memory adapts to make it more accessible in the future.
These characteristics have two important implications:
- Existing knowledge facilitates thinking and learning.
- Once something is learned it is difficult to unlearn it, whether or not it is correct.
Experts and novices
An expert is someone who has a good mastery of knowledge and capabilities in a given area. There is no line separating experts from novices, but rather it is a continuous gradient, students are at different levels at different times.
But their way of thinking and reasoning is also different because of the structure in their long-term memory. Experts automate knowledge and processes and have the ability to see beyond in certain scenarios.
Experts can’t think like novices or novices like experts. This point is critical in understanding how students deal with learning because understanding it is essential to helping them reason, acquire new knowledge, and deal with problem-solving.
What are students thinking about?
Students remember the things that they pay attention to, which leads us to wonder if motivation is a direct path to learning. For the author, it is more important to turn students’ attention to the elements of learning than to create an environment that motivates them. The reason is simple, if the situation created to motivate them leads them to focus on components other than what we want, the path to learning is blurred.
Increase working memory capacity
An increase in the working memory results in better storage and information processing capacity. This favors thinking and learning but it is not as simple as it sounds. Training the brain to increase working memory in certain areas (information that is written, oral…) may not be comparable to other areas, such as solving complex mathematical problems.
So the goal should be to make sure that the working memory is filled with the necessary elements of the specific learning domain.
Methods that last
It is difficult to know when to “transform” a mathematical procedure, which takes away some formalities, to make it more understandable for students. The questions that the author proposes to us, in order to be able to fine-tune this, are: How long will this method last? How are they going to evolve from this method? Is it built on solid mathematical foundations?
If necessary, it is better to teach them a method that may be more difficult in the beginning but has long-term benefits.
Mathematics anxiety
The definition of mathematics anxiety is “the feeling of tension, apprehension, or fear that interferes with mathematical performance.” And it’s not unique to students who aren’t good at math, anyone can suffer from it.
Those who suffer from mathematics anxiety avoid math. It is not closely related to intelligence but rather there is decreased mathematical performance because the anxiety takes up space in working memory. Timed testing seems to cause anxiety and it is hard to clearly differentiate between math anxiety and poor math competence when working with complex problems.
Craig proposes four strategies to help reduce mathematics anxiety in students:
- Ensure that they master and automate basic skills.
- Focus on teacher training.
- Establish varying times for tests.
- Think carefully about what you say to a student who is struggling. It is very important to focus on the capacity of the student to improve work, effort, and guide them with effective study strategies.
At Smartick we believe in evidence-based education. We study and learn about educational research in order to offer a scientifically based method of learning mathematics that helps our students understand and enjoy mathematics.
Learn More:
- Cognitive Load Theory and Multimedia Learning
- How Smartick Virtual World Games Might Help Your Child’s Math Achievement
- The Role of Working Memory in Learning Mathematics
- Word Problems: Levels of Difficulty in Mathematical Language
- Cognitive Flexibility Games with SmartickBrain








Good presentation, it helped me to find out the relationship between thinking and learning