Mar25
Examples of 3rd Grade Math Word Problems with Solutions

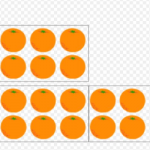
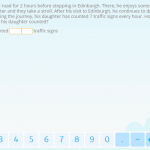
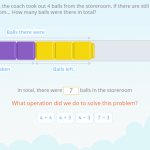
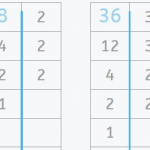
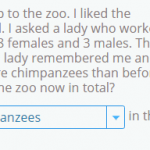
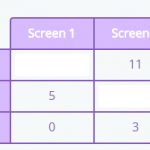
In this post, we are going to look at a selection of 3rd grade math word problems in Smartick. We’ll begin by explaining what a word problem is. What is a Word Problem? A word problem is a question or approach, that cannot be answered using one specific operation, but rather a combination of previous […]
Continue reading »