The essence of mathematics is not to make simple things complicated, but to make complicated things simple.
– S. Gudder
Today we are going to see an interesting strategy, that you may not know about, to solve problems of addition and subtraction of natural numbers. It is called a fact family, and it is a strategy that helps us memorize basic numerical facts and what they are always going to equal. But, what is it exactly?
It is a collection of operations that uses the same numbers. In each fact family there are three numbers that you can add and subtract in various ways.
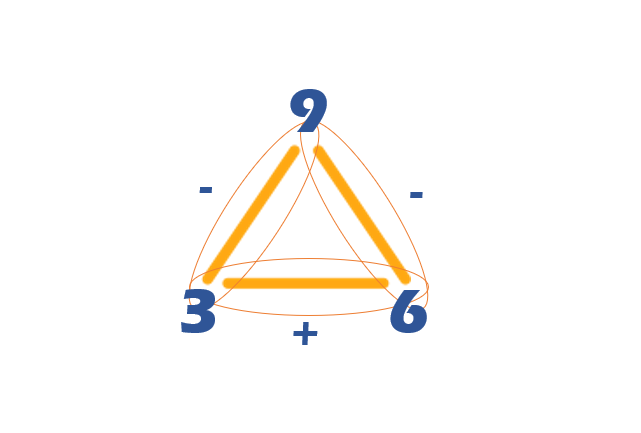
For example, we can form a fact family with these three numbers: 3, 6, and 9 in the following way:
3 + 6 = 9
6 + 3 = 9
9 – 6 = 3
9 – 3 = 6
This allows us to understand that:
- A close relationship exists between addition and subtraction, if we know 6 + 3 = 9, then we also know that 9 – 6 = 3 and that 9 – 3 = 6.
- If we add 6 + 3, we will get the same result as when we add 3 + 6. This is to say that it does not matter how we write the addends, because the result will always be the same.
Now, we will solve a subtraction problem using two digits from the fact family:
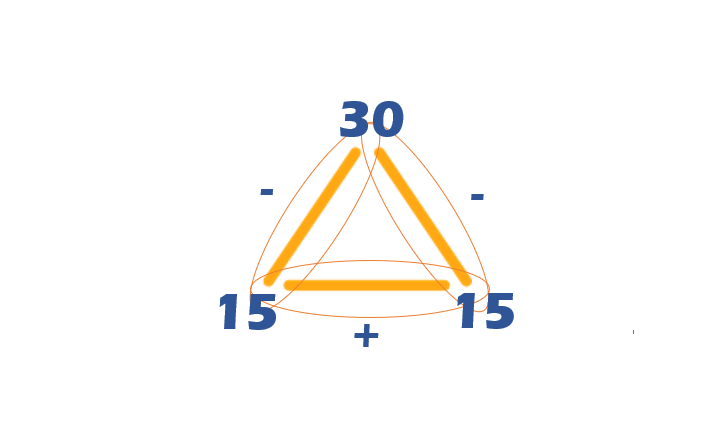
I have a collection of all types of books at my house: picture books, story books, coloring books … I also have 30 comic books in the collection. If I give David 15 comic books as a present… how many comic books will I have left in my collection?
We can represent the operation like this: 30 – 15 = ?
But, through the fact family formula we can reorganize the terms and change the signs, and we get two possibilities:
15 + __ = 30
__ + 15 = 30
What number added to 15 gives us 30? 15! In that case, this means that 30 – 15 is equal to 15 because it is a numerical term from our fact family whose terms are always related.
Now you try with these two problems and check that you know how to do it well together with Smartick:
- Somewhere in Africa there is a very rare and beautiful flower that can live, in total, for 25 years. In a documentary I saw one of these flowers and they said that it had been alive for 17 years. How many more years could it live?
- I love the movie theater and now that I am on vacation and have a lot of time, I want to watch all 49 movies that I have in my house. I am going to watch one movie each day. If I have seen 20…how many movies do I have left to watch?
Learn More:
- Learn about the Distributive Property of Multiplication
- Introduction to Sets and Subsets
- Learn How to Subtract with Examples
- Learn How to Use Roman Numerals
- Solve and Analyze Numerical Place Values
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.