Do you know how to solve a subtraction problem with regrouping? Do you know how regrouping is done and why?
Today we are going to review how to subtract by regrouping and understand why it is done this way.
So that we can picture it better, we are going to do a subtraction with regrouping with the help of drawings. For example, let’s solve the following subtraction:
21 – 16 =?
First, we are going to represent the minuend and the subtrahend with cubes.
Minuend:
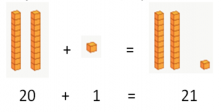 Subtrahend:
Subtrahend:
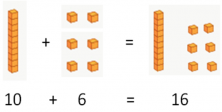 Now we put the minuend and the subtrahend in place.
Now we put the minuend and the subtrahend in place.
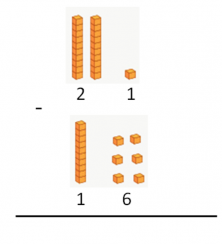
The first thing we do is subtract the units. Since 1 is smaller than 6, we cannot subtract. We have to convert the 1 into a number that is greater than 6; that’s why we remove a ten from the minuend and regroup it with the units:
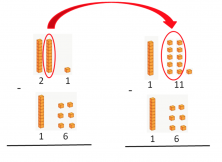
Now we have 11 – 6, which you can subtract. 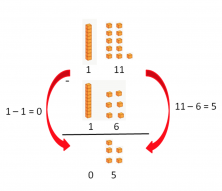 Let’s look at another example:
Let’s look at another example:
33 – 5 =?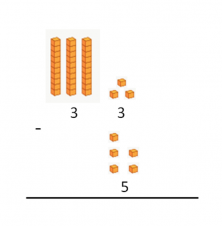
Since 3 is smaller than 5, we cannot subtract the units yet. So we take a ten from the minuend and regroup it with the units. This way we will be able to perform the subtraction: 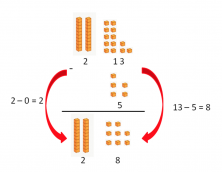 In summary… Whenever the number that we are going to subtract is greater than the number it is being subtracted from, we should add 10 to the units and subtract 1 from the tens digit of the minuend…and this is how to solve subtractions with regrouping!
In summary… Whenever the number that we are going to subtract is greater than the number it is being subtracted from, we should add 10 to the units and subtract 1 from the tens digit of the minuend…and this is how to solve subtractions with regrouping!
If you have enjoyed this post, share it with your friends. And remember that in Smartick you will be able to learn to do all types of subtractions and much more…
If you still have not done it, register for Smartick and try it for free.
Learn More:
- Subtraction with Borrowing: An Explanation of Two Different Algorithms
- Subtraction With and Without Carrying
- Learn How to Subtract without Regrouping
- Mental Calculation: Horizontal Addition and Subtraction
- How to Solve an Addition Problem with Regrouping








Got it! Good info. thanks